Прогиб балки онлайн: Расчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность.

alexxlab

Содержание

Подбор сечения балок онлайн — Мастер Фломастер

При проектировании и изготовлении конструкций из металла и других материалов очень важно соблюдать и выполнять физико-механические расчеты на прочность, одним из которых является расчет балок на изгиб (прогиб). Выполнять расчет прогиба балки онлайн — очень удобно и быстро. Поэтому специалисты нашего предприятия подготовили онлайн калькулятор для расчетов.

Расчет прогиба балки онлайн

Площадь поперечного сечения профиля:

Расчетный вес профиля (балки):

Описание

При выборе схемы с распределенной нагрузкой, приложенная «Нагрузка Q» указывается как относительная «килограмм на метр». Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].

Использование калькулятора «Расчет прогиба балки онлайн» значительно сократит время и послужит залогом надежных инженерных конструкций.

Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.

Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек «звездочка» справа вверху браузера)

По полученному значению требуемого момента сопротивления из сортамента принимаем сечение прокатного двутавра балочного по ГОСТ 26020-83 — №35Б2:

момент инерции относительно оси х

вес 1 погонного метра балки

радиус закругления проката

По принятым характеристикам поперечного сечения двутавра уточняем значение коэффициента для расчета на прочность элементов стальных конструкций с учетом развития пластических деформаций.

Определяем :

Согласно табл. Н.1 ДБН интерполяцией определяем =1,089

Проверка прочности балки

Проверка жесткости балки настила:

Сечение подобрано верно: двутавр балочный по ГОСТ 26020-83 I №35Б2

4.

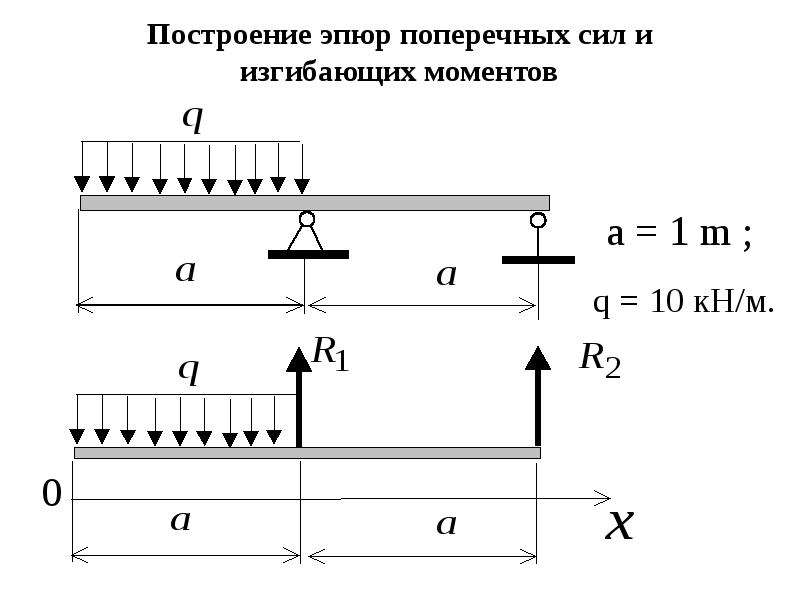Расчет главной балки:

Материал главных балок — сталь С245 по ГОСТ 27772-88 с расчетным сопротивлением стали Ry = 240МПа — для листовой стали толщиной до 20мм.

Сбор нагрузок на главную балку:

В связи с частым расположением балок настила нагрузку на главную балку принимаем равномерно распределенной:

n1=1,2 и n2 =1,05 — к-ты надежности по нагрузке для временной и постоянной

г.б = 2…6 кН/м – предварительный вес главной балки.

Принимаем г.б = 3 кН/м

q н = [19+1,218+3] ∙ 7 = 162,5 кН/м

q р = [1,2 ∙ 19+1,05 ∙ 1,218+1,05 ∙ 3] ∙ 7 = 190,60 кН/м

В связи с тем, что расположение балок настила частое, нагрузку на главную балку принимаем равномерно распределенную.

Определение расчетных усилий:

Упрощенно принимаем нагрузку на балку равномерно распределенной и

определяем расчетный и нормативный изгибающий момент.

Определение расчетных усилий

Расчетный изгибающий момент в балке:

Нормативный изгибающий момент в балке:

Расчетная поперечная сила в балке:

Подбор сечения:

Подбор сечения. Главную балку принимаем постоянного сечения по длине и рассчитываем без учета развития пластических деформаций.

Ry – расчетное сопротивление стали. Ry = 240 МПа = 24 кН/см 2 .

Определяем высоту балки. Задаемся предварительно толщиной стенки по эмпирической формуле:

Оптимальная высота главной балки:

Минимальная высота сечения балки:

где — — предельный относительный прогиб для главных балок.

Высоту балки стремимся принять близкую к оптимальной, но не менее минимальной. Окончательную высоту балки принимаем кратной модулю 100мм или с учетом ширины листов, поставляемых по сортаменту.

Принимаем высоту стенки балки hw= 1240мм из прокатной стали 1250х12

Суммарную толщину полок — 2 x 30 = 60мм;

Общую высоту балки h = 1300мм.

Минимальная толщина стенки из условия среза:

Принимаем окончательно толщину стенки балки равной tw= 12мм.

Компоновка поперечного сечения и определение геометрических размеров:

Определяем площадь полок балки (необходимую площадь пояса).

Принимаем пояс из универсальной широкополочной стали сечением

Отношение соответствует диапазону

Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки и позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с готовым решением. Удачи!

Расчет прогиба балки на двух опорах

Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

  • Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
  • Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
  • Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Методика выполнения расчета на прогиб

Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.

Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.

В нашем случае балка:

  1. Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
  2. Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
  3. Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.

Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.

Вычисляем моменты инерции и сил

Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е). Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).

Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.

Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е).

Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил Mmax = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h2/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.

Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L2/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.

Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h3/12, где b и h – размеры сечения балки.

Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.

Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.

Формулы для практического использования

На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.

Совет! В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.

Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.

Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:

  • Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
  • По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
  • По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.

Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L2/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.

Ответ  прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.

Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.

Заключение

Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.

Что еще почитать по теме?

Автор статьи:

Сергей Новожилов — эксперт по кровельным материалам с 9-летним опытом практической работы в области инженерных решений в строительстве.

Понравилась статья? Поделись с друзьями в социальных сетях:

Facebook

Twitter

Вконтакте

Одноклассники

Google+

Пример решения задачи по сопромату

Ниже приведено условие и решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.

    Определить прогиб свободного конца балки переменного сечения.

     Дано : F=20 кН ; q=8 кН/м ; k=10 ; a=2 м ; b=1.1 м.

                                                                        Решение.

    Определим прогиб свободного конца балки.

    Построим эпюру изгибающих моментов для данного состояния балки. Определим выражения для изгибающих моментов для каждого участка в общем виде. Балка имеет два участка. Обозначим расстояние zi от точки А до некоторого сечения, получим :

    На участке AB (ход справа) :

               0≤z1≤b  ;      M1=-Fz1

    На участке BC (ход справа) :

               b≤z2≤a+b  ;  M2=-Fz2-0.5q(z2-b)2

    Определяем значения изгибающих моментов в характерных точках балки.

    Участок AB : при z1=0 ; MA=0 ;

                            при z1=b ; MBпр=-Fb=-20×1.1=-22 кН·м

    Участок BC : при z2=b ; MBл=-Fb=-20×1.1=-22 кН·м ;

                            при z2=a+b  ; MC=-F(a+b)-0.5qa2=-20×(2+1.1)-0.5×8×22=-80 кН·м

    На участке AB эпюра ограничена прямой линией, на участке BC эпюра ограничена параболой.

    Поперечная сила на участке BC :

               <0

    Таким образом, на участке BC эпюра не имеет экстремума, так как поперечная сила, на этом участке, не меняет знак.

    По полученным данным строим эпюру изгибающих моментов со стороны растянутых волокон.        

    Рассмотрим балку в состоянии P1 под действием только сосредоточенной силы , приложенной в точке А. 

    Для построения эпюры МP1 найдём значения изгибающих моментов в характерных сечениях.

          MA=0  ; MB=-P1b=-1.1 ; MC=-P1(a+b)=-3.2

    По этим данным строим эпюру MP1 со стороны растянутых волокон.

    Определим прогиб свободного конца балки Δ1q по формуле Мора с помощью правила Верещагина. При этом криволинейную эпюру Mq на участке BC , можно представить в виде сложения двух эпюр, как показано на рисунке. Стрелка  f=qa2/8=8×22/8=4 кН·м.   Δ1q==+

    +.                   

    Знак «плюс» означает, что точка А перемещается вниз (в сторону действия ).

   

    Ответ : Δ1q=.

 

Расчет уголка на прогиб и изгиб

Стальной уголок – наиболее востребованный вид фасонного проката. По способу производства он разделяется на горячекатаный и гнутый. Исходные материалы: углеродистые стали обыкновенного качества Ст3 пс/сп (для рядового применения), качественные, низколегированные 09Г2С, 17Г1С, 10ХСНД, 15 ХСНД (для изделий, используемых при повышенных нагрузках, в сложных температурных условиях, при контакте с агрессивными средами).

Калькулятор

Пример расчета

Калькуляторы по теме:

  • Сбор нагрузок на балки перекрытия онлайн.
  • Расчет прямоугольной трубы
  • Расчет квадратной трубы
  • Расчет двутавра
  • Расчет швеллера
  • Расчет деревянной балки

Знакомьтесь: уголок усиленный!

Крепежный уголок — самый простой и надежный элемент крепления. С помощью него можно прикрепить полку на стене, образовать каркас кровати, установить стропильную систему крыши, сконструировать лестничный подъем, закрепить систему инженерных труб, сформировать короб для обшивки гипсокартонными листами.

В любом из этих вариантов, если на конструкцию воздействуют большие нагрузки, стоит важная задача — обеспечение надежности и прочности! Как вариант можно установить уголки непрерывным чередом; тогда это скажется и на стоимости работы, и на внешнем виде узла соединения. Для придания повышенной несущей способности в конструкцию уголка добавлено ребро жесткости. Этот элемент проходит посередине крепежа по обоим его стенкам.

Уголок крепежный усиленный является улучшенной версией стандартного уголка крепежного. Наличие в конструкции уголка ребра жесткости позволяет применять его при соединении несущих деревянных конструкций. Такие элементы обычно имеют большие габариты и вес в стропильной системе, и требуют более надежного крепежа.

Инструкция к калькулятору

Обращаю ваше внимание, что в нецелых числах необходимо ставить точку, а не запятую, то есть, например, 5.7 м, а не 5,7. Также, если что-то не понятно, задавайте свои вопросы через форму комментариев, расположенную в самом низу.

Исходные данные

Расчетная схема:

Длина пролета (L) — расстояние между двумя опорами или от жесткой заделки до края консоли.

Расстояния (А и В) — расстояния от опор до места приложения сил. В случае с 3-ей схемой — расстояние от опоры до края консоли.

Нормативная и расчетная нагрузки — нагрузки, которые действуют на уголок, выраженные в кг/м или кг.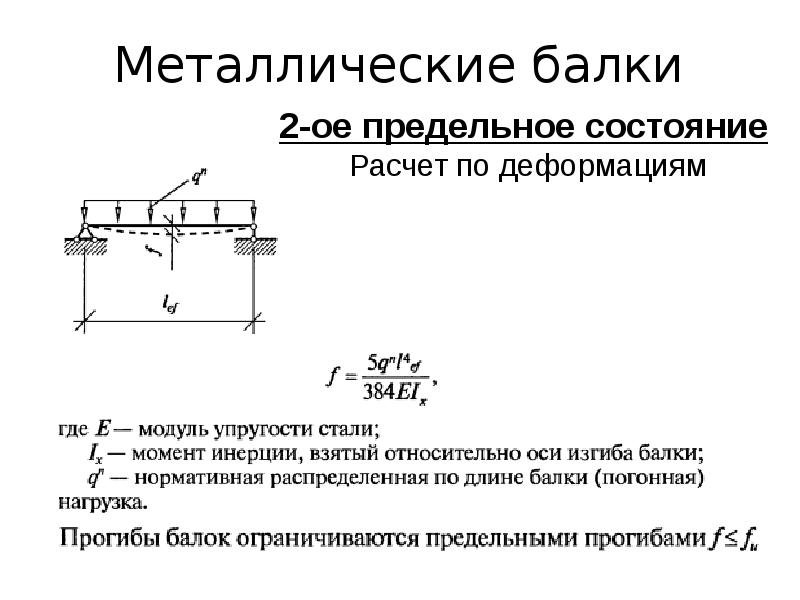

Fmax — максимально допустимый прогиб для балки, применяемый в той или иной конструкции. Можно найти в таблице Е.1 приложения Е СНиПа 2.01.07-85* (СП 20.13330.2011) «Нагрузки и воздействия». Данный показатель для наиболее часто встречающегося случая представлен в таблице 1.

Количество уголков — если Вы собираетесь в качестве балки использовать два спаренных уголка, то нужно выбирать «два», в противном случае «один».

Характеристики стали:

Расчетное сопротивление (Ry) — подбирается в зависимости от марки стали. Но чаще всего проектировщики принимают Ry = 210 МПа. Остальные см. таблицу 2.

Размеры уголка — выбирается предполагаемый размер равнополочного и (или) неравнополочного уголка.

Расположение — выбирается для неравнополочного уголка в зависимости от того, как он будет работать.

По Х — если нагрузка будет приходиться на короткую полку.

По Y — если нагрузка будет приходиться на длинную полку.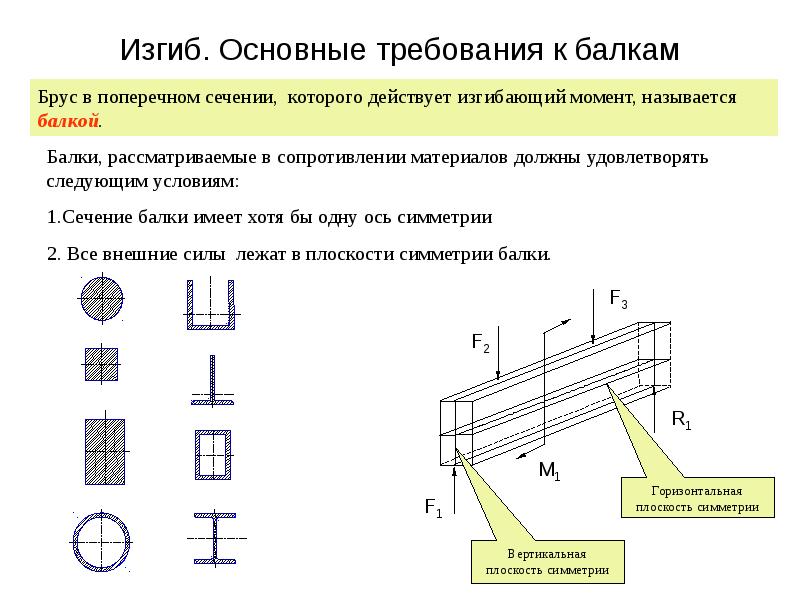

Характеристика стального уголка

Продукт изготавливается высокой точности марки «А» и обычной – марки «В». Могут быть ограниченной длины, немерной, кратной и мерной. Готовый профиль допускает максимальную длину 12 метров. Неравнополочные бывают длиннее. Преимущества металлического изделия:

  • возможное использование в местах со свободным пространством для оборудования и людей;
  • стойкость к коррозии и атмосферному воздействию;
  • высокое качество, прочность и жёсткость;
  • большой срок службы;
  • универсальность;
  • отсутствие скручивания вокруг продольной оси.

Способы расчета металлического уголка, таблица весов, особенности продукции

Стальной уголок – наиболее востребованный вид фасонного проката. По способу производства он разделяется на горячекатаный и гнутый. Исходные материалы: углеродистые стали обыкновенного качества Ст3 пс/сп (для рядового применения), качественные, низколегированные 09Г2С, 17Г1С, 10ХСНД, 15 ХСНД (для изделий, используемых при повышенных нагрузках, в сложных температурных условиях, при контакте с агрессивными средами).

Характеристики горячекатаного металлического уголка

Равнополочный горячекатаный стальной уголок производят в соответствии с ГОСТом 8509-93 из квадрата, являющегося исходной заготовкой. Наиболее массово используется угловой профиль обычной точности «В», для ответственных конструкций – продукция высокой точности «А». Размеры полки, согласно стандарту, – от 20 до 250 мм.

Сортамент неравнополочных уголков определяется ГОСТом 8510-86. Наименьшие размеры полок – 16 и 25 мм, максимальные – 125 и 200 мм. Эта продукция применяется при создании конструкций сложной формы, например, арок.

Для горячекатаной продукции характерна высокая прочность, что позволяет использовать ее в конструкциях, предназначенных для работы в условиях высоких нагрузок. В производстве углового профиля массово используют углеродистую сталь обыкновенного качества и качественную. Изделия из низколегированных сталей применяют для создания конструкций ответственного назначения корпусов, рам и других деталей сельскохозяйственной техники, локомотивов, вагонов, крупногабаритных строительных машин и механизмов. Изделия из такого профиля могут сохранять рабочие характеристики в широком температурном интервале – от -70° до +70°C, при серьезных суточных и сезонных температурных перепадах.

Вместе с типами, существуют четыре схемы нагрузок:

  • Шарнир-Шарнир
  • Заделка-Шарнир
  • Заделка-Заделка»
  • Свободный конец

Наш онлайн калькулятор позволяет сделать расчет, комбинируя все виды балок, типы и схемы нагрузок, при этом абсолютно исключив вероятность допущения ошибки в процессе расчета. Обычно рассчитывают деревянные балки, а также металлические. В процессе вычисления показателя определяется сумма сил, воздействующих на балку, которые направлены перпендикулярно конструкции. Расчет деревянной балки на прогиб осуществляется с учетом материала, т.е. учитывают вид древесины, её гибкость и многие другие параметры, также важно учесть форму сечения балки и нагрузка какого вида оказывается на балку. Сравнивая с расчетом балки из древесины, расчет металлической балки на прогиб существенно отличается, поскольку важное внимание уделяют виду соединения: электросварка, заклепки, болты и другие виды соединений.

Все перечисленные выше нюансы позволяют понять, что расчет балки на прогиб — крайне ответственный этап в процессе стройки какого-либо объекта. От него зависит надежность, долговечность и целостность всей конструкции. Наш калькулятор позволит Вам быстро и безошибочно провести предельно точный расчет.

Квадратные столбы еще имеют ряд недостатков

  • конструкция получается очень трудоемкая, так как необходимо не только обеспечить вертикальное положение столбов, но и нахождение одной из их граней в плоскости забора;
  • так как вес квадратной трубы на 30% больше, чем круглой, то ее стоимость дороже на 35%;
  • сварной шов, присутствующий в трубах с квадратным сечением по всей их длине, служит местом активного развития коррозийных процессов, которым не мешает даже окраска.

Поэтому мы рекомендуем для заборных столбов выбирать столбы из трубы НКТ б/у с круглым сечением и с как можно большей толщиной стенки. Отлично, если эти трубы будут выполнены по бесшовной технологии.

Лаги к круглым столбам прикрепляются внахлест с помощи двух коротких швов по верхнему и нижнему краю лаги. Такие соединения не продуваются, служат долго, а от коррозии их можно защитить при помощи краски. Сварной шов в этом случае очень прочный, а силовая конструкция забора обладает максимальной жесткостью за счет того, что лаги не приходится разрезать. Кроме того, отдельные столбы не выпирают в этом случае из земли.

Расчет уголка на прогиб и изгиб

Данный онлайн-калькулятор предназначен для того, чтобы Вы могли легко и быстро подобрать размеры уголка в зависимости от приходящейся на него нагрузки. Особенность его в том, что на одной странице возможно сравнение равнополочных (ГОСТ 8509-93) и неравнополочных (ГОСТ 8510-86) уголков. Последние, в свою очередь, можно подбирать в зависимости от расположения его в пространстве, т.е. в зависимости от того, как он будет ориентирован относительно нагрузки.

Расчет уголков производится на изгиб и прогиб (по прочности и по деформациям) для следующих расчетных схем:

  • Тип 1 – однопролетная шарнирно-опертая балка с равномерно распределенной нагрузкой. Пример: перемычка из уголка, которая несет плиты перекрытия и небольшую высоту кладки. (Подробнее о расчете перемычек из уголка см. этот калькулятор).
  • Тип 2 – консольная балка с жесткой заделкой с равномерно распределенной нагрузкой. Пример: железобетонный козырек, выполненный с применением уголка, который жестко (с применением ребер жесткости, ограничивающих любые повороты) приварен к железобетонной стене.
  • Тип 3 – однопролетная шарнирно-опертая балка с консолью с равномерно распределенной нагрузкой. Пример: тот же козырек, что и в предыдущей схеме, только здесь уголок с одной стороны заводится в стену, а с другой опирается на раскос (на рисунке синий).
  • Тип 4 – однопролетная шарнирно-опертая балка с одной сосредоточенной силой. Пример: перемычка, на которую опирается одна балка перекрытия.
  • Тип 5 – однопролетная шарнирно-опертая балка с двумя сосредоточенными силами. Пример: перемычка, на которую опираются две сосредоточенные силы.
  • Тип 6 – консольная балка с одной сосредоточенной силой. Пример: козырек дома с кирпичной стенкой на нем, построенного в африканской республике (где никогда не выпадает снег) по фантазии африканского архитектора. Уголки этого козырька жестко заделаны в стену, так как описано во второй схеме.

Примечание: рассчитываемый уголок на рисунках с примерами окрашен в красный цвет.

Расчет уголка на прогиб и изгиб

С помощью данного калькулятора Вы можете не только легко рассчитать уголок на прогиб и изгиб, но и подобрать оптимальный из равнополочного и неравнополочного уголков.

построение эпюр в балках

Расчетная схема № 274130

Почему не бесплатно?

– Сайт создан исключительно на энтузиазме автора и дабы этот энтузиазм не угас, хотелось бы его подкрепить хоть каким-нибудь материальным поощрением. Кроме того, возросшее количество пользователей вынудило перейти на платный хостинг.

А Ваш сайт не сворует мой номер карты, пароли и т.д.

– Это невозможно! После того, как Вы нажмете «Перевести», Вы будете направлены на страницу Яндекса (можете проверить в адресной строке), и все дальнейшие операции будете производить на сервисе Яндекса, так что со стороны сайта Вам ничего не грозит.

Жесткая заделка
Шарнирная опора
Врезной шарнир
Сосредоточенная сила F
Сосредоточенный момент M
Распределенная нагрузка

Калькулятор балок – расчет для разнотипных конструкций

Балки в доме относятся обычно к стропильной системе или перекрытию, и, чтобы получить надежную конструкцию, эксплуатация которой может осуществляться без каких-либо опасений, необходимо использовать калькулятор балок.

На чем строится калькулятор балок

Когда стены уже подведены под второй этаж или под крышу, необходимо сделать перекрытие, во втором случае плавно переходящее в стропильные ноги. При этом материалы нужно подобрать так, чтобы и нагрузка на кирпичные либо бревенчатые стены не превышала допустимую, и прочность конструкции была на должном уровне. Следовательно, если вы собираетесь использовать древесину, нужно правильно подобрать балки из нее, сделать расчеты для выяснения нужной толщины и достаточной длины.

Калькулятор балок

Проседанию или частичному разрушению перекрытия могут послужить разные причины, например, слишком большой шаг между лагами, прогиб поперечин, слишком малая площадь их сечения или дефекты в структуре. Чтобы исключить возможные эксцессы, следует выяснить предполагаемую нагрузку на перекрытие, будь оно цокольное или межэтажное, после чего используем калькулятор балок, учитывая их собственную массу. Последняя может меняться в бетонных перемычках, вес которых зависит от плотности армирования, для дерева и металла при определенной геометрии масса постоянна. Исключением бывает отсыревшая древесина, которую не используют в строительных работах без предварительной сушки.

На балочные системы в перекрытиях и стропильных конструкциях оказывают нагрузку силы, действующие на изгиб сечения, на кручение, на прогиб по длине. Для стропил также нужно предусмотреть снеговую и ветровую нагрузку, которые также создают определенные усилия, прилагаемые к балкам. Также нужно точно определить необходимый шаг между перемычками, поскольку слишком большое количество поперечин приведет к лишней массе перекрытия (или кровли), а слишком малое, как было сказано выше, ослабит конструкцию.

Как рассчитать нагрузку на балку перекрытия

Расстояние между стенами называется пролетом, и в помещении их насчитывается два, причем один пролет обязательно будет меньше другого, если форма комнаты не квадратная. Перемычки межэтажного или чердачного перекрытия следует укладывать по более короткому пролету, оптимальная длина которого – от 3 до 4 метров. При большем расстоянии могут потребоваться балки нестандартных размеров, что приведет к некоторой зыбкости настила. Оптимальным выходом в этом случае будет использование металлических поперечин.

Что касается сечения деревянного бруса, есть определенный стандарт, требующий, чтобы стороны балки соотносились как 7:5, то есть высота делится на 7 частей, и 5 из них должны составить ширину профиля. В этом случае деформация сечения исключается, если же отклониться от вышеуказанных показателей, то при ширине, превышающей высоту, получится прогиб, либо, при обратном несоответствии – загиб в сторону. Чтобы подобное не получилось из-за чрезмерной длины бруса, нужно знать, как рассчитать нагрузку на балку. В частности, допустимый прогиб вычисляется из соотношения к длине перемычки, как 1:200, то есть должен составлять 2 сантиметра на 4 метра.

Чтобы брус не провисал под тяжестью лагов и настила, а также предметов интерьера, можно выточить его снизу на несколько сантиметров, придав форму арки, в этом случае его высота должна иметь соответствующий запас.

Теперь обратимся к формулам. Тот же прогиб, о котором говорилось ранее, рассчитывается так: fнор = L/200, где L – длина пролета, а 200 – допустимое расстояние в сантиметрах на каждую единицу проседания бруса. Для железобетонной балки, распределенная нагрузка q на которую обычно приравнивается 400 кг/м 2 , расчет предельного изгибающего момента выполняется по формуле Мmax = (q · L 2 )/8.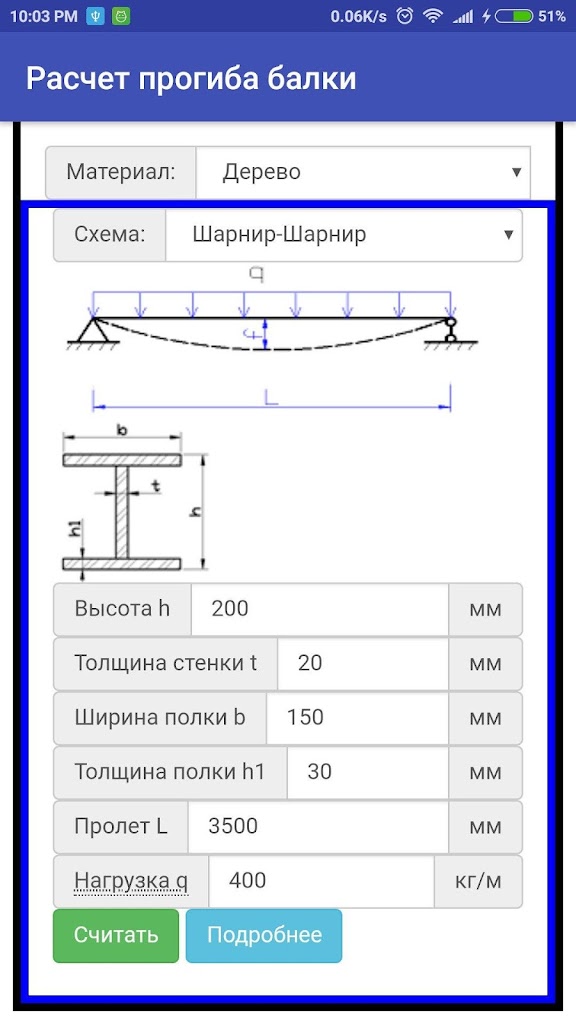 При этом количество арматуры и ее вес определяется по следующей таблице:

Площади поперечных сечений и масса арматурных стержней

Калькулятор балок – расчет для разнотипных конструкций

Безопасность в доме – это не только видеонаблюдение, но и прочные стены с перекрытиями, а значит, во время строительства не лишне использовать калькулятор балок

Пример расчета прогиба балки — Яхт клуб Ост-Вест

Для строительства прочного, надежного и долговечного здания, нужно знать такой показатель, как прогиб балки (формула), то есть величину жесткости.

Данное направление изучается в таких науках (дисциплинах), как “Сопротивление материалов”, “Теория прочности”, “Механика строительная” и прочее.

Прочность и жесткость балки

Современные строительные технологии, применяемые для просчета стройконструкций, называемых также стержневыми, по качествам прочности и жесткости дают уникальную возможность на первом же этапе проектировки вычислить величину прогиба.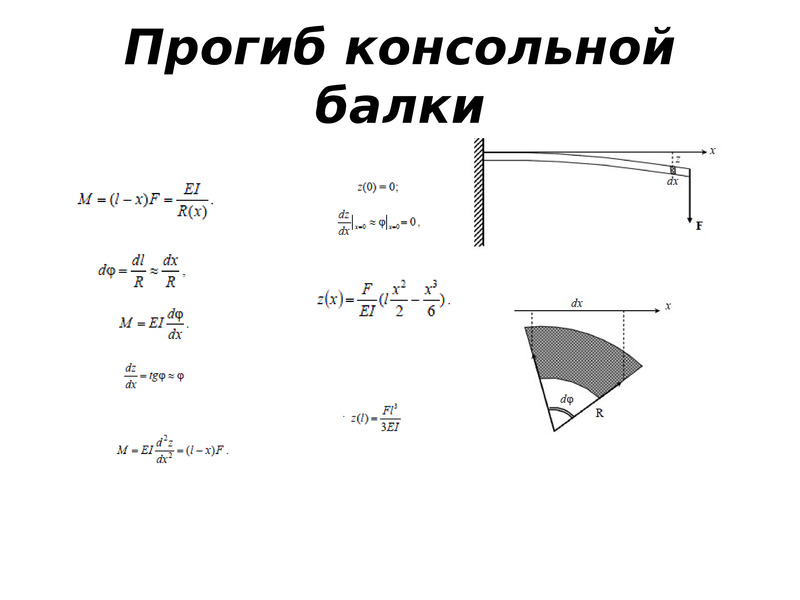

Кроме этого, можно, опираясь на рассчитанные данные, составить заключение о вероятности использования строительной конструкции.

Какой вопрос позволяет решать указанная далее формула для расчета жесткости? Данные, полученные таким путем, говорят о самых больших изменениях в геометрии детали, что могут возникнуть в строительной конструкции.

Несмотря на некоторую бюрократизацию методик для вычисления прогиба, используются опытные формулы, а если воздействие реальных нагрузок отличается от идеальных или усредненных, вопрос решается введением дополнительных коэффициентов для запаса прочности. Понятия «жесткость» и «прочность» связаны и абсолютно неразделимы.

Хотя некоторые различия все-таки есть. Но только в том случае, если рассматривать данные показатели в автомашинах. В стройконструкциях главное нарушение конструкции объектов случается потому, что снижаются или нивелируются полностью вопросы, связанные с запасом прочности, вследствие чего здания нельзя эксплуатировать.

Деревянные балки из древесины хвойных пород

На сегодня в таких предметах изучения, как «Сопромат» и другие, приняты 2 метода для расчета прочности и жесткости:

  • Простой. При просчитывании показателей на основе этого метода используют увеличенный коэффициент.
  • Точный. Тут используются не только коэффициенты, показывающие запас прочности, но также осуществляется вычисление пограничного состояния (какую нагрузку может выдержать балка).

Как рассчитывать прогиб для балки дома

Чтобы просчитать, подходит ли конкретная балка для строительства дома, нужно знать такие показатели:

  • M – это тот максимальный момент, который возникает в балке, находящийся по эпюру моментов. Эпюр – это специальный чертеж с изображением пространственная фигура изображается на плоскости.
  • W n, mіn – момент сопротивления сечения (его значение находят по таблице).
  • Ry – сопротивление, что оказывает материал, из которого изготовлен элемент конструкции дома, изгибаясь от нагрузки.
  • Уc – дополнительный показатель (его можно найти в одной из многочисленных таблиц строительных нормативов).

Формула для расчета прогиба представляет из себя неравенство следующего вида (формула № 1):

Чтобы правильно применить формулу, нужно действовать так:

  • Нарисовать схематично балку и ее будущее расположение под крышей дома. Чтобы верно изобразить на чертеже все части исследуемого объекта, нужно знать форму и линейные размеры балки, поперечного сечения, характер будущих нагрузок, материал, из которого балка изготовлена.
  • Записать ее точные размеры.
  • Рассчитать по указанной формуле, чему равно частное максимального момента балки к произведению остальных трех величин.
  • Сравнить полученный результат с единицей: если он меньше или равен 1, то вычисления дают положительный ответ.

Зная значение параметров рассматриваемой балки и сил, действующих на нее, сделав нехитрые вычисления, можно быстро справится с задачей вычисления допустимого прогиба балки дома.

Как вычислить вспомогательные величины

Для получения полной информации о значениях, необходимых для достижения конечной цели вычислений, нужно узнать, каков момент сопротивление сечения (формула № 2):

Необходимо обязательно уитывать ориентирование рассматриваемого балочного сечения, так как с уменьшением моментов инерций жесткость балок снижается, чего допускать нельзя. Для выяснения максимального значения нагрузки f, которое может выдержать балка, надо вычислить его по такой формуле № 3:

f = (5 / 384) * [(qn * L 4 ) / (E * J)] £ [¦], где

  • L – продольный размер, в метрах
  • E – коэффициент, показывающий упругость (для каждого материала или сплава он будет разным)
  • J – момент инерции по сечению
  • qn – это нагрузка, равномерно-распространенная, выражается в кг/м или в Н/м

Показатель J рассчитывается так:

  • b – диаметр сечений
  • h – вертикальный размер сечения

Примером для сечений, величиной 15 на 20 сантиметров:

J = 0,15 * (0,2) 3 / 12 = 10 000 см 4 или 0,0001 м 4

Кроме указанных расчетных или табличных величин, среди важных факторов, которые нужно учитывать при определении максимальных нагрузок, выделяют такие: статические (которые действуют постоянно, независимо от переменных внешних факторов), периодические (действие ветра, вибрации, ударов).

Пример подсчета прогиба

Прогиб балки (формула, пример расчета) вычисляется так. Допустим, есть балка, для которой нужно рассчитать прогиб, с такими параметрами:

  • Материал изготовления – дерево.
  • Плотность 600 кг/м 3 .
  • Длина балки L – 4 м, остальные размеры: 15 см х 20 см.
  • Масса перекрывающих элементов – 60 кг/м².
  • Максимальная нагрузка q равна 249 кг/м.
  • E (насколько упруго дерево) – 100 000 кгс/ м².
  • J балок – 10 кг*м².

Максимально допустимая нагрузка вычисляется с учетом веса не только балочной конструкции, но и перекрытия, а также опор.

Расчет на поперечный прогиб

Не лишним будет учесть тяжесть, которую будут оказывать люди или приборы, механизмы и другие тяжелые вещи, если вычисляется прогиб балок этажа дома. Нужны такие данные, как:

  • Сколько весит один пог. метр рассматриваемой балки.
  • Сколько весит каждый м 2 перекрытия.
  • Какова временная нагрузка на перекрытие.
  • Сколько составляет нагрузка от перегородок на 1 м 2 перекрытия.
  • Каков коэфф. k (это промежуток, оставляемый между балками).

Чтобы упростить пример расчетов, принимают масс перекрытия за 60 кг/м², нормальную непостоянную нагрузку на каждое перекрытие – 250 кг/м², нагрузки от перегородок равными 75 кг/м², тяжесть части деревянных балок – 18 кг/погонный метр. Когда расстояние между перекрытиями равно составляет 600 мм, тогда коэффициент k равен 0,6. Подставляем в формулу все эти значения:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Изгибающий момент нужно вычислить по формуле №3, учитывая все указанные выше данные. Получается:

f = (5 / 384) * [(qn * L 4 ) / (E * J)] = (5 / 384) * [(249 * 4 4 ) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Это – показатель уровня прогиба во время воздействия максимальной нагрузки. Что именно он обозначает? Получается, что менее, чем на один сантиметр прогнется балка при указанной максимальной нагрузке. После этого нужно сравнить полученный результат с единицей: 0,83 меньше 1.

При расчетах деформации важных строящегося здания используют указанные выше простые формулы. Прогиб балки по формуле СНиП является универсальным способом вычисления жесткости балок и величины их прогибания.

Как посчитать балку на изгиб — на видео:

Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

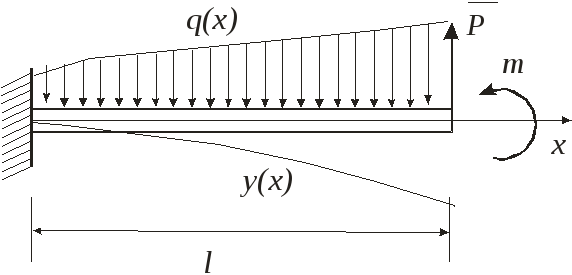
Для заданной балки двутаврового сечения ( = 210 МПа, Е = 2 х 10 5 МПа) и нагрузок требуется;

1. Построить эпюры поперечных сил и изгибающих моментов;

2. Определить нормальные и касательные напряжения в сечениях с наибольшим моментом и поперечной силой на расстоянии h/4 от нейтральной оси;

3. Определить прогиб конца балки точки В.

При построении эпюр Q и М необходимо соблюдать правило зна­ков. Положительное направление сил показано на схеме.

1. Определяем опорные реакции

2. Методом сечений определяем ординаты поперечной силы в характерных сечениях. Для этого балку разбиваем на два участка. Границы участков – места изменения нагрузки. Построение эпюры на­чинаем с правого свободного конца балки.

Максимум изгибавшего момента находится в сечении, где поперечная сила равна нулю. Положение этого сечения определяем из условия:

3. Методом сечений определяем изгибающие моменты в характерных сечениях и строим эпюру моментов. Экстремум в т. х = 2 м.

Наиболее нагруженным сечением в балке является сечение А у заделки, где Мmax = 120 кН м, Qmах = – 80 кН.

4. Из условий прочности по нормальным напряжениям определяем требуемый момент сопротивления сечения.

По сортаменту ГОСТ 8509-72 принимаем двутавр № 33.

Максимальные напряжения в опасном сечении будут равны

5. Определяем нормальное напряжение в точке Е сечения на расстоянии h/4 = 8,25 см от нейтральной оси (рис. 4.9.).

Для определения касательного напряжения в точке Е вычислим статический момент отсеченной выше точки Е площади относительно центральной оси Х.

6. Определяем прогиб балки в точке В, используя универсаль­ное уравнение прогибов

Для заданной консольной балки граничные условия будут: угол поворота сечения А ; прогиб сечения А

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 9825 – | 7406 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

  • Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
  • Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
  • Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Методика выполнения расчета на прогиб

Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.

Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.

В нашем случае балка:

  1. Имеет прямоугольное сечение S=b*h , длина опирающейся части составляет L ;
  2. Линейка нагружена силой Q , проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ , с прогибом относительно начального горизонтального положения, равным f ;
  3. Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.

Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ , где Е – справочная величина, R — усилие, Δ — величина деформации тела.

Вычисляем моменты инерции и сил

Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е) . Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е) .

Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.

Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е) .

Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил Mmax = q*L*2/8 , соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е) . Величину b·h 2 /6 называют моментом инерции и обозначают W . В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.

Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L 2 /8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.

Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h 3 /12, где b и h – размеры сечения балки.

Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.

Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.

Формулы для практического использования

На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.

Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.

Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:

  • Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
  • По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
  • По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.

Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L 2 /(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.

Ответ прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.

Заключение

Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.

Калькулятор фиксированной балки

| calcresource

Теоретические основы

Содержание

Введение

Фиксированная балка (также называемая фиксированной балкой) является одной из самых простых конструкций.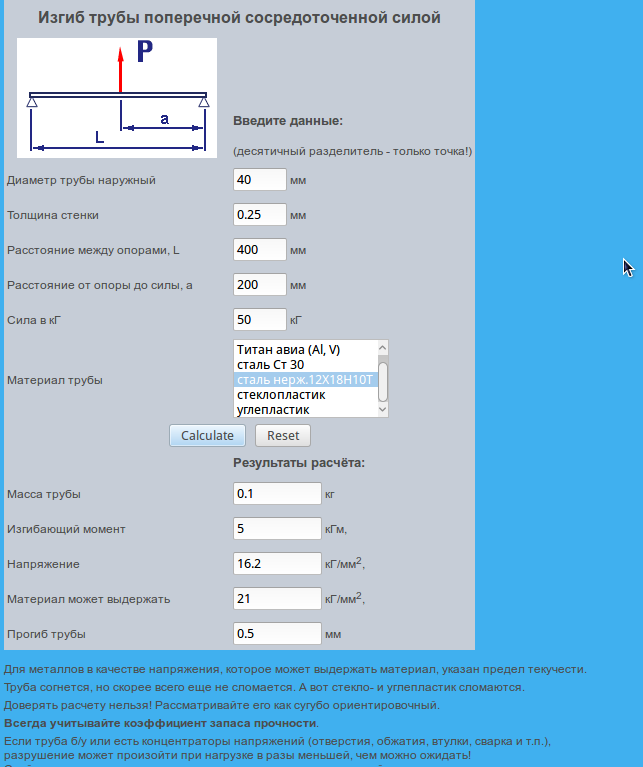 У него всего две опоры, обе фиксированные. Фиксированные опоры запрещают любое движение, включая вертикальные или горизонтальные смещения, а также вращения. Ограничение вращения приводит к нулевому уклону на двух концах, как показано на следующем рисунке.

Фиксированная балка имеет две фиксированные опоры, по одной на каждом конце.

Фиксированная балка имеет больше опор, чем требуется для обеспечения статической прочности. В самом деле, вторую неподвижную опору можно полностью удалить, превратив конструкцию в консольную балку, которая по-прежнему является конструкцией, несущей звуковые нагрузки. Другими словами, фиксированная балка обеспечивает избыточность опор. Напротив, конструкция без избыточности превратилась бы в механизм, если бы какая-либо из ее опор была удалена. В этой ситуации конструкция может беспрепятственно перемещаться в одном или нескольких направлениях.Структуры, которые не предлагают избыточности, называются критическими или детерминантными структурами . Если с ними произойдет локальный сбой, они рухнут. Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной структурой. Избыточные структуры могут выдержать один или несколько локальных сбоев, прежде чем они станут механизмами. Фиксированная балка — это неопределенная (или дублирующая) конструкция.

Допущения

Обычно при выполнении статического анализа несущей конструкции необходимо рассчитать внутренние силы и моменты, а также прогибы. Когда конструкция является 2-мерной, а приложенные нагрузки действуют в одной и той же 2D-плоскости, есть только три результирующих действия, представляющих интерес:

  1. осевые силы N,
  2. поперечные силы сдвига V и изгиб
  3. . моменты M.

Для неподвижной балки, нагруженной только поперечными нагрузками (так, чтобы их направление было перпендикулярно продольной оси балки), осевая сила всегда равна нулю, при условии, что прогибы остаются небольшими. Поэтому осевыми силами обычно можно пренебречь.

Результирующие характеристики реакции и прогибы, представленные на этой странице, рассчитаны с учетом следующих допущений:

  • Материал однороден и изотропен (другими словами, его характеристики одинаковы в любой точке и в любом направлении)
  • Материал является линейно упругим
  • Нагрузки прикладываются статично (они не меняются со временем)
  • Поперечное сечение одинаково по всей длине балки
  • Прогибы небольшие
  • Каждое поперечное сечение, которое изначально является плоским и также перпендикулярно продольной оси, остается плоским и перпендикулярно отклоненной оси.Это тот случай, когда высота поперечного сечения намного меньше длины балки (в 10 и более раз), а также поперечное сечение не является многослойным (не сечение сэндвич-типа).

Последние два предположения удовлетворяют кинематическим требованиям теории пучка Эйлера-Бернулли и здесь также приняты.

Условные обозначения

Условные обозначения необходимы для расчета внутренних сил и моментов N, V, M и их физической интерпретации в любом сечении балки. Здесь приняты следующие правила:

  1. Осевая сила N считается положительной, когда она вызывает растяжение детали.
  2. Сдвигающая сила V положительна, когда она вызывает вращение детали по часовой стрелке.
  3. Изгибающий момент M является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.

Эти правила хотя и не являются обязательными, но достаточно универсальны. Другой набор правил, если следовать ему последовательно, также даст те же физические результаты.

Положительный знак для внутренней осевой силы, N, поперечной силы, V и изгибающего момента, M

Обозначения
  • E: модуль упругости материала (модуль Юнга)
  • I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
  • L: общий пролет балки
  • R: реакция опорной силы
  • d: прогиб
  • M: изгибающий момент и опорный момент
  • V: поперечная поперечная сила
  • \ theta: наклон
  • w: распределенная нагрузка
  • W: общая сила распределенной нагрузки
  • P: точечная нагрузка

Неподвижная балка с равномерно распределенной нагрузкой

В этом случае нагрузка w распределяется равномерно по всему пролету балки, имея постоянная величина и направление.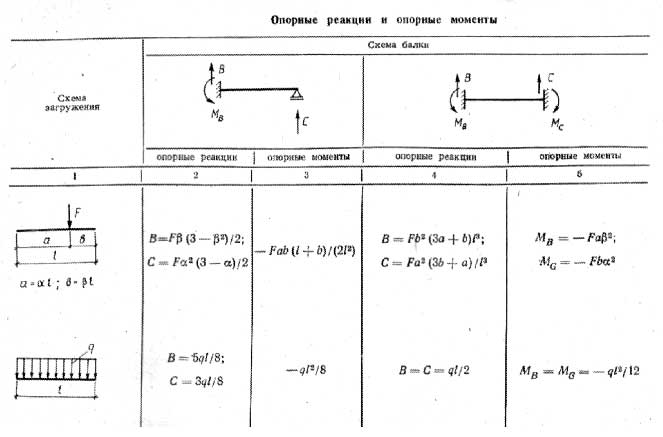 4} {384 EI}

Точки контра-изгиба:

(нулевой момент)

x_o = \ left (3- \ sqrt {3} \ over6 \ right) L \ ок0.2)

Неподвижная балка с точечной силой в середине

В этом случае сила сосредоточена в одной точке, расположенной в середине балки. Однако на практике сила могла быть применена на ограниченном протяжении. В непосредственной близости от приложения силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным. Однако это только местное явление. По мере удаления от места действия силы результаты становятся действительными в силу принципа Сен-Венана при условии, что нагруженная площадь остается существенно меньше общей длины балки.

В следующей таблице представлены формулы, описывающие статический отклик фиксированной балки с закрепленными обоими концами под действием сосредоточенной точечной силы P, приложенной посередине.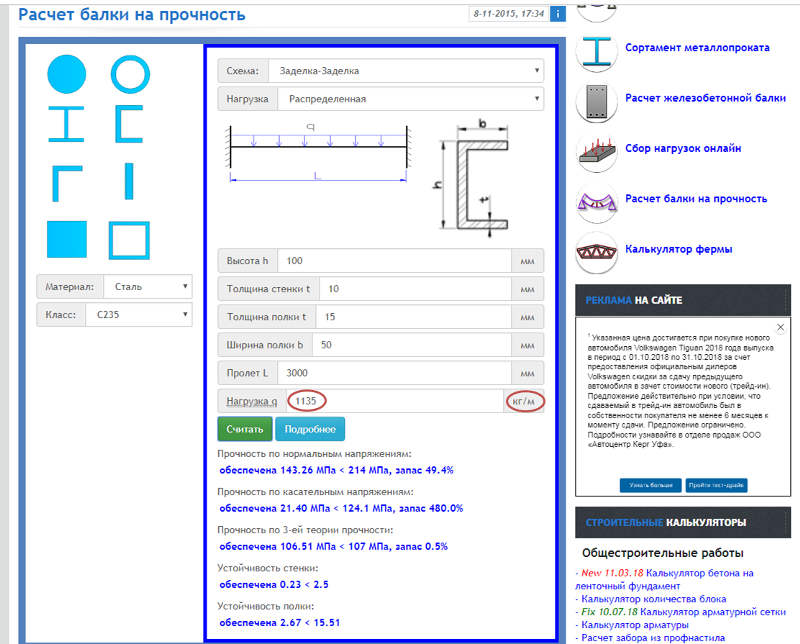 3} {192 EI}

Точки обратного изгиба:

(нулевой момент)

x_o = {L \ over 4}

x_1 = {3L \ over 4}

Изгибающий момент в точке x: M (x) = \ left \ {\ begin {align} & — {PL \ over8} + {Px \ over2} &, x \ le L / 2 \\ & — {PL \ over8} + {P (L-x) \ over2} &, x> L / 2 \ end {align} \ right.2 \ left (4x-L \ right)} {48 E I} &, x> L / 2 \ end {align} \ right. Наклон в точке x: \ theta (x) = \ left \ {\ begin {align} — & \ frac {Px (L-2x)} {8 EI} &, x \ le L / 2 \ \ — & \ frac {P (Lx) (L — 2x)} {8 EI} &, x> L / 2 \ end {align} \ right.

Неподвижная балка с точечной силой в произвольном положении

В этом случае сила сосредоточена в одной точке в любом месте пролета балки. Однако на практике сила может быть применена на небольшой площади, а не в идеальной точке.Однако, чтобы считать силу сосредоточенной, размеры зоны нагружения должны быть значительно меньше общей длины балки. В непосредственной близости от силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным. Однако это только местное явление. По мере удаления от места расположения силы расхождение результатов становится незначительным.

В следующей таблице представлены формулы, описывающие статический отклик фиксированной балки с закрепленными обоими концами под действием сосредоточенной точечной силы P, приложенной на случайном расстоянии a от левого конца.2 \ over 2EI} &, x> a \ end {align} \ right.

где:

b = La

s_a = L + 2a

s_b = L + 2b

Неподвижная балка с точечным моментом

В этом случае момент накладывается на единичный точку балки в любом месте пролета балки. С практической точки зрения, это может быть пара сил или элемент на кручение, соединенный из плоскости и перпендикулярно балке, как показано на следующем рисунке.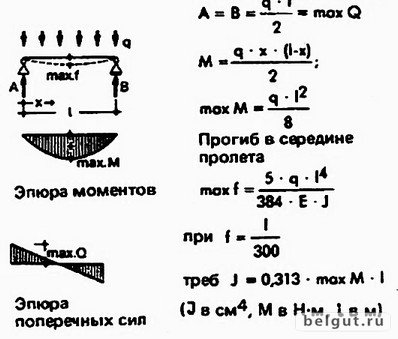

На практике момент не может быть испытан на идеально бесконечно малой точке.Вместо этого небольшая длина балки будет подвергаться действию приложенного момента. В непосредственной близости от области нагружения ожидается, что результаты, предсказанные с помощью классической теории балок, будут неточными (из-за концентраций напряжений и других локализованных эффектов). Однако по мере того, как мы уходим, предсказанные результаты становятся совершенно достоверными, как указано в принципе Сен-Венана, при условии, что площадь нагрузки остается существенно меньше, чем общая длина балки.

В следующей таблице представлены формулы, описывающие статический отклик фиксированной балки с закрепленными обоими концами под действием сосредоточенного момента M точки, приложенного на расстоянии a от левого конца.2} {2 E I} + {M_Ax \ over E I} — {M (x-a) \ over E I} &, x> a \ end {align} \ right.

где:

b = La

x_1 = L \ left ({1 \ over2} — {\ sqrt {3} \ over 6} \ right) \ приблизительно 0,21132L

x_2 = L \ left ({1 \ over2} + {\ sqrt {3} \ over 6} \ right) \ приблизительно 0,78868L

t_a = L-3a

t_b = L-3b

Фиксированная балка с треугольной нагрузкой

В этом случае нагрузка распределяется по всему пролету балки, однако ее величина непостоянна. Вместо этого он изменяется линейно, начиная с нуля на левом фиксированном конце, постепенно увеличиваясь до своего пикового значения w_1 на правом фиксированном конце. Размеры w_1 — сила на длину. Общее количество силы, приложенной к балке, равно W = {1 \ over2} w L, где L — длина пролета. В некоторых случаях может быть задана полная сила W, а не пиковая сила на длину, w_1.

Ориентация треугольной нагрузки важна для использования стола! Формулы были подготовлены для случая восходящей нагрузки (слева направо), как показано на схеме.Для нисходящей нагрузки вы можете отразить балку так, чтобы ее левый конец (точка A) был наименее загруженным, и, следовательно, ось x и соответствующие результаты также должны быть отражены.

В следующей таблице представлены формулы, описывающие статический отклик фиксированной балки с закрепленными обоими концами при линейно изменяющейся (треугольной) распределенной нагрузке, восходящей слева направо.

Неподвижная балка с линейно изменяющейся распределенной нагрузкой (треугольная)
Количество Формула
Реакции:

R_A = {3w_L11 \ over208} over20}

M_A = — {w_1L ^ 2 \ over30}

M_B = — {w_1L ^ 2 \ over20}

Концевые уклоны: \ theta_A = \ theta_B = 0
Предельный изгибающий момент : M_u = — {w_1L ^ 2 \ over20}
Предельная сила сдвига: V_u = — {7w_1L \ over20}
Предельное отклонение: d_u = \ frac {Cw_1 L ^ 4} {100000 EI}
Изгибающий момент при x: M (x) = — {w_1 \ left (2L ^ 3 -9L ^ 2x + 10x ^ 3 \ right) \ over60L}
Сдвигающее усилие при x: V (x) = {w_1 \ left (3L ^ 2 — 10x ^ 2 \ right) \ over20L}
Прогиб в x: d (x) = — \ frac {R_A x ^ 3 } {6 EI} — {M_Ax ^ 2 \ over 2EI} + \ frac {w_1x ^ 5} {120EIL}
Наклон в точке x: \ theta (x) = \ frac {R_A x ^ 2} {2 EI} + { M_A x \ over EI} — \ frac {w_1x ^ 4} {24EIL}

где:

C = (15 — \ sqrt {105}) (\ sqrt {105} -5) ^ 2 \ приблизительно 130.8538

Неподвижная балка с трапециевидной нагрузкой

В этом случае нагрузка распределяется по всему пролету балки с линейно изменяющейся величиной, начиная с w_1 на левом фиксированном конце и до w_2 на правом фиксированном конце . Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, составляет: W = {L \ over2} (w_1 + w_2), где L — длина балки.

Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго.Они могут принимать даже отрицательные значения (одно или оба).

В следующей таблице представлены формулы, описывающие статический отклик фиксированной балки с закрепленными обоими концами при переменной распределенной нагрузке трапециевидной формы.

Неподвижная балка с линейно изменяющейся распределенной нагрузкой (VDL)
Кол-во Формула
Реакции:

R_A = {Lw (7w) \ более чем 3 R_B = {L (3w_1 + 7w_2) \ over20}

M_A = -L ^ 2 ({w_1 \ over20} + {w_2 \ over30})

M_B = -L ^ 2 ({w_1 \ over30} + {w_2 \ over20})

Концевые уклоны: \ theta_A = \ theta_B = 0
Изгибающий момент в x: M (x) = M_A + R_Ax — {(2w_1 + w_x) x ^ 2 \ over6}
Сила сдвига в точке x: V (x) = R_A — {(w_1 + w_x) x \ over2}
Прогиб в точке x: d (x) = — \ frac { R_A x ^ 3} {6 EI} — {M_Ax ^ 2 \ over 2EI} + \ frac {(4w_1 + w_x) x ^ 4} {120EI}
Наклон в точке x: \ theta (x) = \ frac {R_A x ^ 2} {2 EI} + {M_Ax \ over EI} — \ frac {(3w_1 + w_x) x ^ 3} {24EI}

где:

w_x = w_1 + {(w_2 -w_1) х \ over L}

Неподвижная балка с трапециевидным распределением нагрузки в виде плиты

Такое распределение нагрузки является обычным для балок по периметру плиты.Распределенная нагрузка имеет трапециевидную форму, как показано на следующем рисунке. Максимальная величина нагрузки w, возникающая внутри балки, в то время как с двух сторон нагрузка линейно изменяется, уменьшаясь до нуля на двух концах. Размеры w — сила на длину. Общее количество силы, приложенной к балке, составляет: W = w (La / 2-b / 2), где L — длина балки, а a, b — длины левой и правой стороны, соответственно, где распределение нагрузки меняется (треугольное ).

Нагрузка неподвижной балки из соседней плиты.Поверхностная нагрузка на выделенную область ложится на ближайшую балку (нижнюю).

В следующей таблице представлены формулы, описывающие статический отклик фиксированной балки с закрепленными обоими концами при трапециевидном распределении нагрузки, как показано на схеме.

Неподвижная балка с трапециевидным распределением нагрузки
Количество Формула
Реакции:

R_B = {w s_1 \ over20L ^ 3} слева L — {a \ over2} — {b \ over2} \ right) — R_B

M_B = — {w s_2 \ over60L ^ 2}

M_A = M_B + R_BL-w \ left ({L ^ 2 \ over2} — {bL \ over2} + {b ^ 2 \ over6} — {a ^ 2 \ over 6} \ right)

Концевые уклоны: \ theta_A = \ theta_B = 0
Изгибающий момент при x: M (x) = \ left \ {\ begin {align} & M_A + R_A x- {wx ^ 3 \ over6a} &, x \ le a \\ & M_A + R_A x- {w (a ^ 2 + 3x ^ 2-3ax) \ over6} &, a

Неподвижная балка с частично распределенной равномерной нагрузкой

В этом случае нагрузка распределяется равномерно только на часть пролета балки, имеющую постоянную величину w. Оставшийся пролет остается свободным от какой-либо нагрузки. Размеры w — сила на длину. Таким образом, общая сила, приложенная к балке, составляет: W = w \ left (L-a-b \ right), где L — длина пролета, а a, b — длина левой и правой стороны, соответственно, при отсутствии нагрузки.

В следующей таблице представлены формулы, описывающие статический отклик фиксированной балки с закрепленными обоими концами при частично распределенной равномерной нагрузке.2)

Неподвижная балка с частично распределенной трапециевидной нагрузкой

В этом случае нагрузка распределяется только на часть длины балки, а оставшаяся длина остается свободной от какой-либо нагрузки. Распределение изменяется линейно по величине от w_1 в левую сторону до w_2 в правую сторону. Размеры w_1 и w_2 — сила на длину. Таким образом, общая сила, приложенная к балке, составляет: W = {L-a-b \ over2} (w_1 + w_2), где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки соответственно.

Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).

Это самый общий случай. Формулы для частично распределенных равномерных и треугольных нагрузок можно получить, соответствующим образом задав значения w_1 и w_2. Кроме того, соответствующие случаи для полностью нагруженного пролета можно получить, установив a и b равными нулю.

В следующей таблице представлены формулы, описывающие статический отклик фиксированной балки с закрепленными обоими концами при частично распределенной трапециевидной нагрузке.3

Статьи по теме

Понравилась эта страница? Поделись с друзьями!

Простой калькулятор отклонения балки

Результаты листинга Простой калькулятор отклонения балки

Калькулятор отклонения балки

9 часов назад Omnicalculator.com Просмотреть все