Содержание
Расчет балки на прогиб — онлайн калькулятор
Онлайн калькулятор по определению прогиба балки.
Для расчета вам необходимо:
1. Выбрать форму поперечного сечения
2. Выбрать материал (при использовании металлических балок — можно использовать сортамент)
3. Выбрать необходимую расчетную схему
4. Выбрать вид нагрузки (распределенная по длине балки либо сосредоточенная)
5. Указать геометрические размеры, указанные на картинках
6. Задать нагрузку (нагрузку можно рассчитать онлайн здесь)
Из возможных поперечных сечений в данном онлайн калькуляторе выбраны само часто встречающиеся сечения: круг, труба, двутавр, швеллер, уголок, прямоугольник, квадрат и профильная труба.
В расчет входят такие материалы как дерево, сталь, железобетон, алюминий, медь и стекло.
Также есть возможность выбора расчетной схемы: шарнир-шарнир, заделка-шарнир, заделка-заделка и заделка-свободный конец.
После того, как прогиб балки рассчитается – появится кнопка Подробнее, нажав на которую, можно узнать площадь сечения рассчитываемого элемента, его массу, распределенную нагрузку от собственного веса и момент инерции заданного сечения).
Зная значение длины пролета балки по СП 20.13330.2016 «Нагрузки и воздействия» для таких конструкций как балка, ферма, ригель, прогон, плита, настил покрытий и перекрытий, рассчитывается предельный прогиб, который можно сравнить с получившимся прогибом и принять решение о сечении вашей конструкции (для уменьшения прогиба в 1-ую очередь надо увеличивать высоту сечения).
При расчете балки программа уже учитывает собственный вес.
Помимо того, что Вы рассчитаете балку на прогиб, нужно ее проверить и на прочность здесь .
Если данный калькулятор оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц.сети, а также посмотреть другие
строительные калькуляторы онлайн, они простые, но здорово облегчают жизнь строителям и тем, кто решил сам строить свой дом с нуля.
Последние изменения:
— Добавлен расчет предельного прогиба балки
— Добавлена возможность загружения балки сосредоточенной силой
— Исправлены графические замечания с расположением швеллера
— Добавлен расчет таврого сечения
— Исправлено положение прямоугольного сечения
— Добавлена возможность поворота швеллера
— Добавлена возможность ввода своих значений модуля упругости и плотности материала
— Исправлено отображение толщины стенки и полки швеллера
Расчёт металлической балки онлайн (калькулятор).
 —
—
Расчет балки онлайн
Для расчета балок первым делом необходимо определить усилия, возникающие в конструкциях. В данном разделе показано, как находить усилия, опорные реакции, прогибы и углы поворота в различных изгибаемых конструкциях. Для самых распространенных из них вы можете воспользоваться онлайн расчетом. Для редких — приведены все формулы определения необходимых значений.
Онлайн расчет балки на двух опорах (калькулятор).
Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.
Синие ячейки — ввод данных. (Белые ячейки — ввод координаты для определения промежуточного итога).
Зеленые ячейки — расчетные, промежуточный итог.
Оранжевые ячейки — максимальные значения.
>>> Перейти к расчету балки на двух опорах <<<
Онлайн расчет консольной балки (калькулятор).
Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.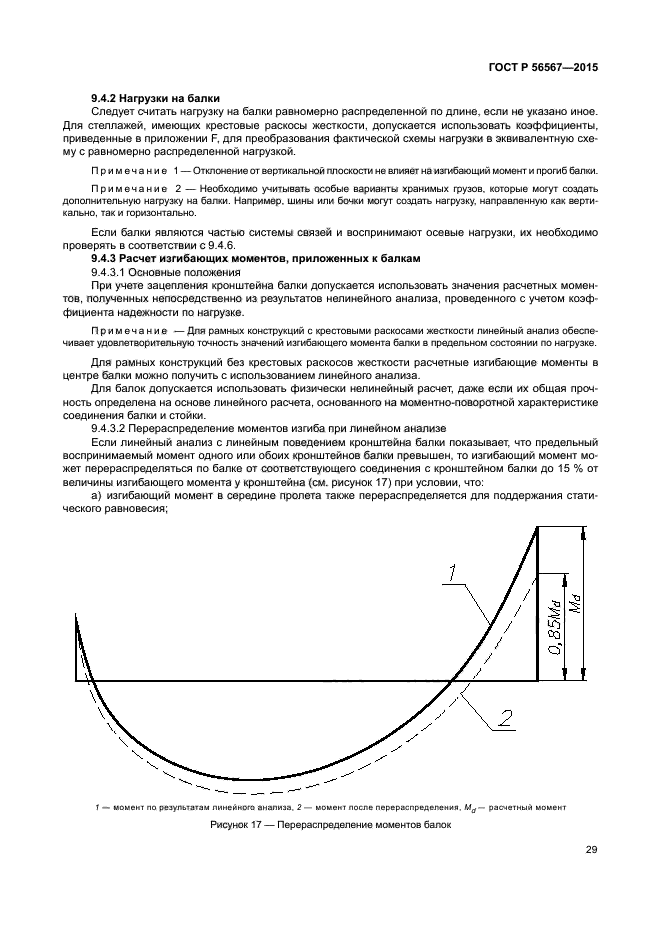
Синие ячейки — ввод данных. (Белые ячейки — ввод координаты для определения промежуточного итога).
Зеленые ячейки — расчетные, промежуточный итог.
Оранжевые ячейки — максимальные значения.
>>> Перейти к расчету консольной балки <<<
Расчет однопролетной балки на двух шарнирных опорах.
Рис.1 Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке
Рис.2 Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках
Рис.3 Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке
Рис4. Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке
Рис5. Расчет балки на двух шарнирных опорах при действии изгибающего момента
Расчет балок с жестким защемлением на двух опорах
Рис6. Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке
Рис7. Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках
Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках
Рис8. Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке
Рис9. Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке
Рис10.Расчет балки с жестким защемлением на опорах при действии изгибающего момента
Расчет консольных балок
Рис11. Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке
Рис12. Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке
Рис13. Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке
Рис14. Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента
Расчет двухпролетных балок
Рис15. Расчет двухпролетной балки с шарнирными опорами при одной сосредоточенной нагрузке
Рис16.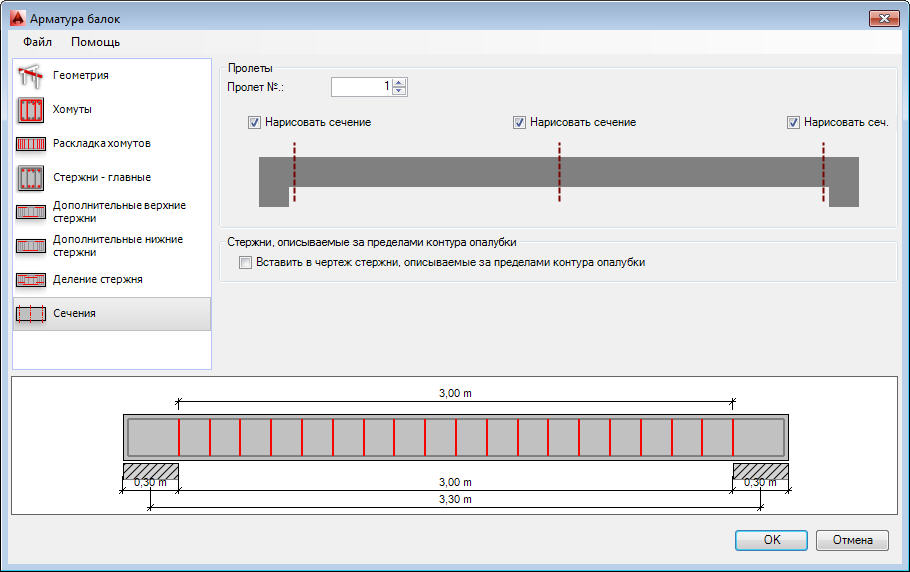 Расчет двухпролетной балки с шарнирными опорами при одной равномерно-распределенной нагрузке
Расчет двухпролетной балки с шарнирными опорами при одной равномерно-распределенной нагрузке
Рис17. Расчет двухпролетной балки с шарнирными опорами при одной неравномерно-распределенной нагрузке
Калькулятор балок – основные расчеты для перекрытий и стропил + видео
Балки в доме относятся обычно к стропильной системе или перекрытию, и, чтобы получить надежную конструкцию, эксплуатация которой может осуществляться без каких-либо опасений, необходимо использовать
калькулятор балок.
На чем строится калькулятор балок
Когда стены уже подведены под второй этаж или под крышу, необходимо сделать перекрытие, во втором случае плавно переходящее в стропильные ноги. При этом материалы нужно подобрать так, чтобы и нагрузка на кирпичные либо бревенчатые стены не превышала допустимую, и прочность конструкции была на должном уровне. Следовательно, если вы собираетесь использовать древесину, нужно правильно подобрать балки из нее, сделать расчеты для выяснения нужной толщины и достаточной длины.
Калькулятор балок
Укажите размеры балок перекрытий и шаг.
Проседанию или частичному разрушению перекрытия могут послужить разные причины, например, слишком большой шаг между лагами, прогиб поперечин, слишком малая площадь их сечения или дефекты в структуре. Чтобы исключить возможные эксцессы, следует выяснить предполагаемую нагрузку на перекрытие, будь оно цокольное или межэтажное, после чего используем калькулятор балок, учитывая их собственную массу. Последняя может меняться в бетонных перемычках, вес которых зависит от плотности армирования, для дерева и металла при определенной геометрии масса постоянна. Исключением бывает отсыревшая древесина, которую не используют в строительных работах без предварительной сушки.
На балочные системы в перекрытиях и стропильных конструкциях оказывают нагрузку силы, действующие на изгиб сечения, на кручение, на прогиб по длине. Для стропил также нужно предусмотреть снеговую и ветровую нагрузку, которые также создают определенные усилия, прилагаемые к балкам. Также нужно точно определить необходимый шаг между перемычками, поскольку слишком большое количество поперечин приведет к лишней массе перекрытия (или кровли), а слишком малое, как было сказано выше, ослабит конструкцию.
Также нужно точно определить необходимый шаг между перемычками, поскольку слишком большое количество поперечин приведет к лишней массе перекрытия (или кровли), а слишком малое, как было сказано выше, ослабит конструкцию.
Вам также может быть интересна статья о расчёте количества необрезной и обрезной доски в кубе: https://remoskop.ru/kolichestvo-dosok-v-kube.html
Как рассчитать нагрузку на балку перекрытия
Расстояние между стенами называется пролетом, и в помещении их насчитывается два, причем один пролет обязательно будет меньше другого, если форма комнаты не квадратная. Перемычки межэтажного или чердачного перекрытия следует укладывать по более короткому пролету, оптимальная длина которого – от 3 до 4 метров. При большем расстоянии могут потребоваться балки нестандартных размеров, что приведет к некоторой зыбкости настила. Оптимальным выходом в этом случае будет использование металлических поперечин.
Оптимальным выходом в этом случае будет использование металлических поперечин.
Что касается сечения деревянного бруса, есть определенный стандарт, требующий, чтобы стороны балки соотносились как 7:5, то есть высота делится на 7 частей, и 5 из них должны составить ширину профиля. В этом случае деформация сечения исключается, если же отклониться от вышеуказанных показателей, то при ширине, превышающей высоту, получится прогиб, либо, при обратном несоответствии – загиб в сторону. Чтобы подобное не получилось из-за чрезмерной длины бруса, нужно знать, как рассчитать нагрузку на балку. В частности, допустимый прогиб вычисляется из соотношения к длине перемычки, как 1:200, то есть должен составлять 2 сантиметра на 4 метра.
Чтобы брус не провисал под тяжестью лагов и настила, а также предметов интерьера, можно выточить его снизу на несколько сантиметров, придав форму арки, в этом случае его высота должна иметь соответствующий запас.
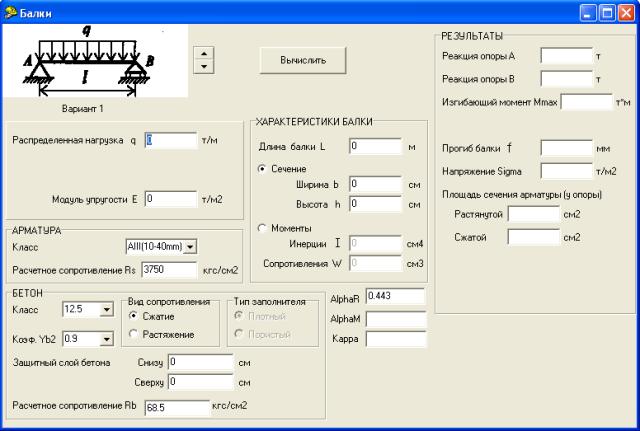
Теперь обратимся к формулам. Тот же прогиб, о котором говорилось ранее, рассчитывается так: fнор = L/200, где L – длина пролета, а 200 – допустимое расстояние в сантиметрах на каждую единицу проседания бруса. Для железобетонной балки, распределенная нагрузка q на которую обычно приравнивается 400 кг/м2, расчет предельного изгибающего момента выполняется по формуле Мmax = (q · L2)/8. При этом количество арматуры и ее вес определяется по следующей таблице:
Тот же прогиб, о котором говорилось ранее, рассчитывается так: fнор = L/200, где L – длина пролета, а 200 – допустимое расстояние в сантиметрах на каждую единицу проседания бруса. Для железобетонной балки, распределенная нагрузка q на которую обычно приравнивается 400 кг/м2, расчет предельного изгибающего момента выполняется по формуле Мmax = (q · L2)/8. При этом количество арматуры и ее вес определяется по следующей таблице:
Площади поперечных сечений и масса арматурных стержней
Диаметр, мм | Площадь поперечного сечения, см2, при числе стержней | Масса 1 пог.м, кг | Диаметр, мм | ||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
Проволочная и стержневая арматура | |||||||||||
3 | 0. | 0.141 | 0.212 | 0.283 | 0.353 | 0.424 | 0.5 | 0.565 | 0.636 | 0.052 | 3 |
4 | 0.126 | 0.25 | 0.38 | 0.5 | 0.68 | 0.75 | 0.88 | 1 | 1.18 | 0.092 | 4 |
5 | 0.196 | 0.39 | 0.59 | 0.79 | 0.98 | 1. | 1.38 | 1.57 | 1.77 | 0.154 | 5 |
6 | 0.283 | 0.57 | 0.85 | 1.13 | 1.42 | 1.7 | 1.98 | 2.26 | 2.55 | 0.222 | 6 |
7 | 0.385 | 0.77 | 1.15 | 1.54 | 1.92 | 2.31 | 2.69 | 3.08 | 3.46 | 0.302 | 7 |
| 8 | 0. | 1.01 | 1.51 | 2.01 | 2.52 | 3.02 | 3.52 | 4.02 | 4.58 | 0.395 | 8 |
9 | 0.636 | 1.27 | 1.91 | 2.54 | 3.18 | 3.82 | 4.45 | 5.09 | 5.72 | 0.499 | 9 |
10 | 0.785 | 1.57 | 2.36 | 3.14 | 3.93 | 4. | 5.5 | 6.28 | 7.07 | 0.617 | 10 |
12 | 1.131 | 2.26 | 3.39 | 4.52 | 5.65 | 6.78 | 7.91 | 9.04 | 10.17 | 0.888 | 12 |
14 | 1.539 | 3.08 | 4.61 | 6.15 | 7.69 | 9.23 | 10.77 | 12.3 | 13.87 | 1.208 | 14 |
16 | 2. | 4.02 | 6.03 | 8.04 | 10.05 | 12.06 | 14.07 | 16.08 | 18.09 | 1.578 | 16 |
18 | 2.545 | 5.09 | 7.63 | 10.17 | 12.7 | 15.26 | 17.8 | 20.36 | 22.9 | 1.998 | 18 |
20 | 3.142 | 6.28 | 9.41 | 12.56 | 15. | 18.84 | 22 | 25.13 | 28.27 | 2.465 | 20 |
22 | 3.801 | 7.6 | 11.4 | 15.2 | 19 | 22.81 | 26.61 | 30.41 | 34.21 | 2.984 | 22 |
25 | 4.909 | 9.82 | 14.73 | 19.64 | 24.54 | 29.45 | 34.36 | 39.27 | 44. | 3.85 | 25 |
28 | 6.153 | 12.32 | 18.47 | 24.63 | 30.79 | 36.95 | 43.1 | 49.26 | 55.42 | 4.83 | 28 |
32 | 8.043 | 16.09 | 24.18 | 32.17 | 40.21 | 48.26 | 56.3 | 64.34 | 72.38 | 6.31 | 32 |
36 | 10. | 20.36 | 30.54 | 40.72 | 50.89 | 61.07 | 71.25 | 81.43 | 91.61 | 7.99 | 36 |
40 | 12.561 | 25.13 | 37.7 | 50.27 | 62.83 | 75.4 | 87.96 | 100.53 | 113.1 | 9.865 | 40 |
45 | 15.904 | 31.81 | 47.71 | 63.62 | 79. | 95.42 | 111.33 | 127.23 | 148.13 | 12.49 | 45 |
50 | 19.635 | 39.27 | 58.91 | 78.54 | 98.18 | 117.81 | 137.45 | 157.08 | 176.72 | 15.41 | 50 |
55 | 23.76 | 47.52 | 71.28 | 95.04 | 118.8 | 142.56 | 166.32 | 190.08 | 213. | 18.65 | 55 |
60 | 28.27 | 56.54 | 84.81 | 113.08 | 141.35 | 169.62 | 197.89 | 226.16 | 254.43 | 22.19 | 60 |
70 | 38.48 | 76.96 | 115.44 | 153.92 | 192.4 | 220.88 | 269.36 | 307.84 | 346.32 | 30.21 | 70 |
80 | 50. | 100.54 | 150.81 | 201.08 | 251.35 | 301.62 | 351.89 | 402.16 | 452.43 | 39.46 | 80 |
Семипроволочные канаты класса К-7 | |||||||||||
4.5 | 0.127 | 0.25 | 0.38 | 0.51 | 0.64 | 0.76 | 0.89 | 1.01 | 1.14 | 0.102 | 4.5 |
6 | 0.226 | 0.45 | 0. | 0.9 | 1.13 | 1.36 | 1.58 | 1.81 | 2.03 | 0.181 | 6 |
7.5 | 0.354 | 0.71 | 1.06 | 1.41 | 1.77 | 2.12 | 2.48 | 2.83 | 3.18 | 0.283 | 7.5 |
9 | 0.509 | 1.02 | 1.53 | 2.04 | 2.54 | 3.05 | 3.56 | 4. | 4.58 | 0.407 | 9 |
12 | 0.908 | 1.82 | 2.72 | 3.63 | 4.54 | 5.45 | 6.35 | 7.26 | 8.17 | 0.724 | 12 |
15 | 1.415 | 2.83 | 4.24 | 5.66 | 7.07 | 8.49 | 9.9 | 11.32 | 12.73 | 1.132 | 15 |
Нагрузка на любую балку из достаточно однородного материала рассчитывается по ряду формул. Для начала высчитывается момент сопротивления W ≥ М/R. Здесь М – это максимальный изгибающий момент прилагаемой нагрузки, а R – расчетное сопротивление, которое берется из справочников в зависимости от используемого материала. Поскольку чаще всего балки имеют прямоугольную форму, момент сопротивления можно рассчитать иначе: Wz = b · h2 /6, где b является шириной балки, а h – высотой.
Для начала высчитывается момент сопротивления W ≥ М/R. Здесь М – это максимальный изгибающий момент прилагаемой нагрузки, а R – расчетное сопротивление, которое берется из справочников в зависимости от используемого материала. Поскольку чаще всего балки имеют прямоугольную форму, момент сопротивления можно рассчитать иначе: Wz = b · h2 /6, где b является шириной балки, а h – высотой.
Что еще следует знать про нагрузки на балку
Перекрытие, как правило, является заодно и полом следующего этажа и потолком предыдущего. А значит, нужно сделать его таким, чтобы не было риска объединить верхние и нижние помещения путем банального перегруза меблировкой. Особенно такая вероятность возникает при слишком большом шаге между балками и отказе от лагов (дощатые полы настилаются прямо на брус, уложенный в пролеты). В этом случае расстояние между поперечинами напрямую зависит от толщины досок, например, если она составляет 28 миллиметров, то длина доски не должна быть более 50 сантиметров. При наличии лагов минимальный промежуток между балками может достигать 1 метра.
В этом случае расстояние между поперечинами напрямую зависит от толщины досок, например, если она составляет 28 миллиметров, то длина доски не должна быть более 50 сантиметров. При наличии лагов минимальный промежуток между балками может достигать 1 метра.
Также обязательно следует учитывать массу утеплителя, используемого для пола. Например, если укладываются маты из минеральной ваты, то квадратный метр цокольного перекрытия будет весить от 90 до 120 килограммов, в зависимости от толщины термоизоляции. Опилкобетон увеличит массу такого же участка в два раза. Использование же керамзита сделает перекрытие еще тяжелее, поскольку на квадратный метр будет приходиться нагрузка в 3 раза больше, чем при укладке минеральной ваты. Далее, не следует забывать про полезную нагрузку, которая для межэтажных перекрытий составляет 150 килограммов на квадратный метр минимум.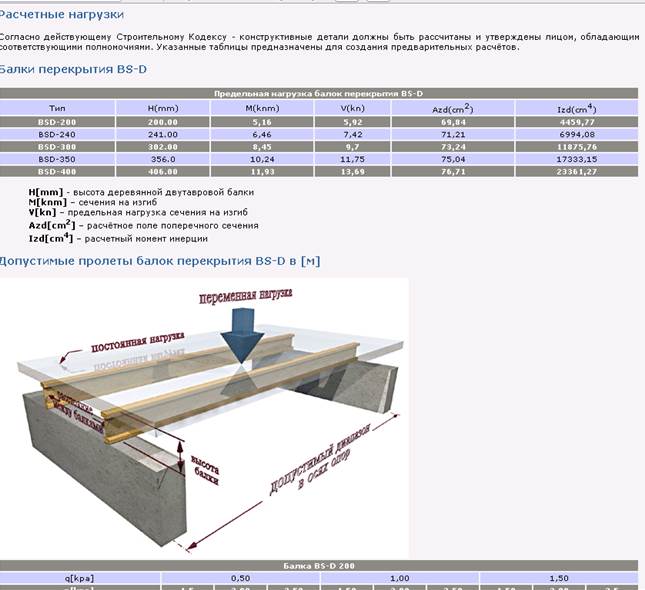 На чердаке достаточно принять допустимую нагрузку в 75 килограммов на квадрат.
На чердаке достаточно принять допустимую нагрузку в 75 килограммов на квадрат.
Оцените статью: Поделитесь с друзьями!
Калькулятор расчета деревянных балок перекрытия и стропильной системы!
Как пользоваться онлайн калькулятором расчета балок перекрытия и стропил
Чтобы правильно произвести прочностной расчет балки перекрытия и подобрать необходимый тип двутавровой балки, вы можете воспользоваться онлайн-калькулятором. На основе полученных вычислений можно точно рассчитать количество, необходимое для устройства стропильной системы или укладки лаг. Расчет деревянных балок перекрытия возможен только после того, как будет известно расстояние между стенами (расчетная длина балки). Кроме того, необходимо знание величины предполагаемой нагрузки на всю конструкцию.
Для межэтажных перекрытий, в том числе цокольного, используйте значение 400 кг/м2; для чердачного — 200 кг/м2 (или 250 кг/м2, если нагрузка от стропильной системы передается непосредственно на чердачное перекрытие). Для стропильной системы 220 кг/м2 для Московского региона, для других регионов принимайте значения в зависимости от снегового района.
Для стропильной системы 220 кг/м2 для Московского региона, для других регионов принимайте значения в зависимости от снегового района.
Заказать бесплатный расчет балок по проекту или проконсультироваться у специалистов нашей компании можно по телефону
+7(495)105-91-63
+7(812)425-65-03
+7(843)207-04-92
+7(4722)77-73-16
+7(800)333-79-86
+7(421)240-08-29
+7(818)246-42-27
+7(861)212-30-63
+7(800)333-37-59
Так же Вы можете прислать чертежи для расчета на [email protected]
Онлайн калькулятор расчета деревянных балок перекрытия и стропил
Где используются балки
ПерекрытиеСтропила
Вам необходимо выбрать конструкцию, для которой вы будете использовать балки: будет ли это расчет перекрытий (применяются в качестве лаг) или стропильной системы (используются в качестве стропил).
Компания «ИнтерСити» производит износоустойчивые деревянные двутавры. Благодаря отличным эксплуатационным свойствам, изделия могут использоваться в различных конструкциях. Однако нужно помнить, что самостоятельно производить расчет балки перекрытия «на глаз» не следует. Ошибка может привести к прогибу конструкции под нагрузкой и, как следствие, потере возможности дальнейшей эксплуатации. Последующий ремонт или замена балок — очень трудоемкий и дорогой процесс. Отнеситесь серьезно к подбору и расчету конструкции перекрытий и стропил; излишняя экономия и подбор без расчета по принципу «всегда так строили» может привести к серьезным проблемам.
Ошибка может привести к прогибу конструкции под нагрузкой и, как следствие, потере возможности дальнейшей эксплуатации. Последующий ремонт или замена балок — очень трудоемкий и дорогой процесс. Отнеситесь серьезно к подбору и расчету конструкции перекрытий и стропил; излишняя экономия и подбор без расчета по принципу «всегда так строили» может привести к серьезным проблемам.
Расчет деревянных балок перекрытий: онлайн калькулятор
Деревянные брусья для перекрытий в частном строительстве используют часто. Легкость, доступность по цене и возможность самостоятельного монтажа компенсируют способность к возгоранию, поражению грибком и гниению. В любом случае при возведению второго и более этажей просто необходимо произвести расчет деревянных балок перекрытия. Онлайн-калькулятор, который мы представляем в этом обзоре, поможет справиться с этой задачей просто и быстро.
Деревянные брусья для перекрытия – только качественная древесина
Читайте в статье
Польза онлайн-калькулятора для расчета деревянных перекрытий
Самостоятельные расчеты утомительны и чреваты риском не учесть какой-либо важный параметр. Так, деревянные балки для перекрытий должны обладать определенным сечением, учитывающим возможную нагрузку на них от мебели и техники, находящихся в помещении людей. При таких расчетах крайне важно знать возможный прогиб балки и максимальное напряжение в опасном сечении.
Так, деревянные балки для перекрытий должны обладать определенным сечением, учитывающим возможную нагрузку на них от мебели и техники, находящихся в помещении людей. При таких расчетах крайне важно знать возможный прогиб балки и максимальное напряжение в опасном сечении.
Разное сечение бруса
Преимущества калькулятора в следующем:
- Точность. Формулы расчета учитывают множество параметров. В специальных полях задаются: тип поперечного сечения (круглое или прямоугольное), длину балки между опорами и шаг, параметры используемой древесины, предполагаемую постоянную нагрузку.
- Сроки. Ввести готовые параметры и получить результат выйдет значительно быстрее, чем рассчитывать вручную требуемые значения.
- Удобство. Онлайн-калькулятор расчета деревянных балок составлен таким образом, что после введения всех постоянных величин, вам остается просто подбирать сечение балки до тех пор, пока не будет обеспечена необходимая прочность.
Расчет деревянного бруса для перекрытия: на что обратить внимание
До расчетов и покупки рекомендовано обратить внимание на типы перекрытий. Брус для надежной связки строительных конструкций, бывает следующих видов:
- Балки. Массив квадратного или прямоугольного сечения, уложенный с шагом от 60 см до 1 м. Стандартная длина – 6 м, на заказ изготавливаются балки до 15 м.
- Ребра. Балки, напоминающие широкую (20 см) и толстую доску (7 см). Шаг укладки на ребро не более 60 см. Стандартная длина – 5 м, под заказ – 12 м.
Ребра перекрытия для одноэтажных построек
- Комбинация двух типов бруса. Наиболее надежные перекрытия, служащие опорой для пролетов, до 15 м.
Сначала определяется прогиб балки, максимальное напряжение в опасном сечении и коэффициент запаса прочности. Если значение коэффициента получается меньше 1, то это значит, что прочность не обеспечена. В этом случае необходимо изменить условия расчета (изменить сечение балки, увеличить или уменьшить шаг, выбрать другую породу древесины и т.д.)
| Длина балок, м | ||||
| Шаг укладки, м | 2,0 | 3,0 | 4,0 | 5,0 |
| 0,6 | 75*100 | 75*200 | 100*200 | 150*225 |
| 1 | 75*150 | 100*175 | 150*200 | 175*250 |
Когда нужное сечение найдено требуется рассчитать его кубатуру. Это произведение длины, ширины и высоты. Далее по проекту находим количество балок перекрытия и умножаем на полученный результат.
Брус
Итог
Важно! Для строительства многоэтажных домов не рекомендовано приобретать балки недостаточной длины. Сращивание, даже качественное, снижает надежность конструкций.
Сращивание двух балок перекрытия = снижение надежности
Для наглядности пользователю предоставлено видео расчета древесины для перекрытий.
ПОНРАВИЛАСЬ СТАТЬЯ? Поддержите нас и поделитесь с друзьями
Расчет балок часть 1 | Онлайн калькулятор
В данном разделе можно выполнить онлайн расчеты статически определимых балок в условиях прямого поперечного изгиба под действием сосредоточенной нагрузки. Расчеты определяют прогиб, угол поворота и изгибающий момент в произвольно заданной точке балки при различных граничных условиях. Определив наибольший изгибающий момент и соответствующее опасное сечение балки легко подобрать его размеры исходя из допускаемых напряжений в сечении.
Исходные данные:
L – длина балки, в миллиметрах;
a – координата точки приложения сосредоточенной нагрузки, в миллиметрах;
X – координата точки нахождения изгибающего момента, угла поворота и прогиба балки, в миллиметрах;
F – нагрузка, в ньютонах;
Ix – момент инерции сечения относительно оси, перпендикулярной действию нагрузки, в метрах 4;
Е – модуль упругости материала балки, в паскалях.
Расчет балки # 1.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке консольно закрепленной балки под действием сосредоточенной нагрузки.
Граничные условия:
RL = 0 – реакция опоры в крайней левой точке;
ML = 0 – изгибающий момент в крайней левой точке;
θR = 0 – угол поворота в крайней правой точке;
YR = 0 – прогиб балки в крайней правой точке.
Расчет балки # 2.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленным концом и скользящей опорой под действием сосредоточенной нагрузки.
Граничные условия:
RL = 0 – реакция опоры в крайней левой точке;
θL = 0 – угол поворота в крайней левой точке;
θR = 0 – угол поворота в крайней правой точке;
YR = 0 – прогиб балки в крайней правой точке.
Расчет балки # 3.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленным концом и шарнирной опорой под действием сосредоточенной нагрузки.
Граничные условия:
МL = 0 – изгибающий момент в крайней левой точке;
YL = 0 – прогиб балки в крайней левой точке;
θR = 0 – угол поворота в крайней правой точке;
YR = 0 – прогиб балки в крайней правой точке.
Расчет балки # 4.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленными концами под действием сосредоточенной нагрузки.
Граничные условия:
θL = 0 – угол поворота в крайней левой точке;
YL = 0 – прогиб балки в крайней левой точке;
θR = 0 – угол поворота в крайней правой точке;
YR = 0 – прогиб балки в крайней правой точке.
Расчет балки # 5.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c шарнирными опорами под действием сосредоточенной нагрузки.
Граничные условия:
МL = 0 – изгибающий момент в крайней левой точке;
YL = 0 – прогиб балки в крайней левой точке;
МR = 0 – изгибающий момент в крайней правой точке;
YR = 0 – прогиб балки в крайней правой точке.
Расчет балки # 6.1
Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c шарнирной и скользящей опорами под действием сосредоточенной нагрузки.
Граничные условия:
RL = 0 – реакция опоры в крайней левой точке;
θL = 0 – угол поворота балки в крайней левой точке;
МR = 0 – изгибающий момент в крайней правой точке;
YR = 0 – прогиб балки в крайней правой точке.
Расчет деревянных балок перекрытия калькулятор онлайн
Сделать надежное перекрытие можно только с правильно подобранным размером балок. Чтобы определить этот самый точный размер потребуется произвести расчет. Это можно сделать с помощью онлайн программы, которая представляет своего рода калькулятор.
Зачем надо рассчитывать?
Вся нагрузка на межэтажное перекрытие, ложится на деревянные балки, поэтому они являются несущими. От прочности балок перекрытия зависит целостность постройки и безопасность находящихся в ней людей.
Производить расчет деревянных элементов необходимо для выяснения допустимой вертикальной нагрузки, действующей на нее. Строительство новой или реконструкция старой постройки без предварительного расчета сечения несет огромный риск.
Выстроенное наугад перекрытие из слабых деревянных балок может в любой момент обрушиться, что приведет к большим финансовым затратам, а еще хуже, к травматизму людей. Взятые с запасом балки большого сечения создадут лишнюю нагрузку на стены и основание постройки.
Кроме определения прочности, существует расчет прогиба деревянных элементов. Он больше определяет эстетичную сторону строения. Даже если крепкая балка перекрытия выдержит припадающий на нее вес, она может прогнуться. Кроме испорченного внешнего вида, прогнувшийся потолок создаст дискомфорт пребывания в такой комнате. По нормам прогиб не должен превышать 1/250 длины балки.
Онлайн расчет
Сделать расчет всех элементов перекрытия можно через онлайн калькулятор. Это специальная программа, позволяющая подсчитать величину прогиба деревянной балки при заданных параметрах, а также определить оптимальное сечение для определенного перекрытия. Использование онлайн расчета поможет перед началом строительства учесть все нагрузки, припадающие на несущие конструкции. Можно сделать расчет нагрузки 1 м опоры и высчитать количество деревянных элементов необходимых для возведения крыши. Работает онлайн калькулятор просто надо лишь правильно внести требуемые данные.
Общая инструкция проведения онлайн расчета
Интерфейс программы довольно прост и с ним может разобраться даже новичок. Калькулятор состоит из маленьких окошек, куда необходимо вводить данные. После нажатия кнопки «рассчитать», пользователь получает готовый результат расчета.
На разных сайтах оформление программы может отличаться, но принцип ее действия одинаков:
- Вначале потребуется выбрать в окошке программы конструкцию, для которой будет производиться расчет деревянных балок. Здесь надо знать ограничение некоторых показателей: максимальная длина элементов перекрытия составляет 12 м, а стропильной системы — 13 м.
- Далее, в программу вводят данные максимального размера пролета между элементами перекрытия или опорами стропильной системы.
- Указывается планируемое расстояние для монтажа балок. Надо учесть, что все десятичные значения в онлайн калькулятор вписывают с точкой, а не с запятой. Возьмем, к примеру, значение 0.9 м.
- Следующими указывают стандартные нагрузки, которые для деревянного перекрытия составляют 400 кг/м2, а для стропильной системы — 220 кг/м2.
- Последнее значение, вводимое в онлайн калькулятор, в градусах указывает наклон стропил.
Введенные в программу данные должны быть точными без погрешностей, иначе результат получится неправильным.
Выполнение расчета в ручном режиме
Многие опытные строители не доверяют подобным онлайн программам, предпочитая использовать для расчета обычный калькулятор. Производя в ручном режиме расчет по деревянным балкам, надо учесть следующие рекомендации:
- Заход деревянных балок сделанных из бруса в бетонной или кирпичной постройке должен составлять не меньше 150 мм. Если вместо бруса используется доска, ее минимальный заход равен 100 мм. По деревянным домам показатель немного другой. Минимальный заход элемента, изготовленного с бруса или доски, составляет 70 мм;
- При использовании металлических крепежей, пролет должен равняться длине конструкции перекрытия. На металлические части припадет вес перекрытия и других элементов;
- Стандартная планировка дома имеет ширину пролета 2,5–4 м. Его можно перекрыть шестиметровым элементом. Большие пролеты перекрывают клееным брусом или выстраивают дополнительные стены-перегородки.
Применяя для расчета обычный калькулятор, эти рекомендации помогут сделать крепкое перекрытие.
Определение нагрузки
Перекрытие совместно с находящимися на нем предметами создает деревянным балкам определенную нагрузку. Точно ее высчитать можно только в проектных организациях. Примерный расчет делают калькулятором, пользуясь следующими рекомендациями:
- Чердаки утепленные минватой и подшитые доской отличаются минимальной нагрузкой, примерно 50 кг/м2. Расчет нагрузки выполняют по формуле: значение запаса прочности — 1,3 умножают на показатель максимальной нагрузки — 70.
- Если вместо минваты применяется более тяжелый теплоизолятор и массивная подшивная доска, нагрузка увеличивается в среднем до 150 кг/м2. Определить общую нагрузку можно следующим образом: значение запаса прочности умножается на средний показатель нагрузки и ко всему приплюсовывается размер требуемой нагрузки.
- Делая расчет для мансарды, нагрузку допускают до 350 кг/м2. Это связно с тем, что добавляется вес пола, мебели и др.
С этим определением разобрались, теперь идем далее.
Определение сечения и шага установки элементов перекрытия
Данный процесс требует придерживаться следующих правил:
- Соотношение ширины к высоте конструкции приравнивается 1,4/1. Следовательно, ширина элементов перекрытия зависит от этого показателя и может варьироваться от 40 до 200 мм. Толщина и высота деревянных элементов зависит от толщины теплоизоляции примерно 100–3000 мм;
- Расстояние между элементами, то есть их шаг, может быть от 300 до 1200 мм. Здесь надо учесть габариты теплоизоляции с подшивочным материалом. В каркасной постройке расстояние между балками приравнивают к шагу каркасных стоек;
- Деревянным балкам допускается небольшой изгиб, который для перекрытия чердака составляет — 1/200, а для межэтажного — 1/350;
- При нагрузке 400 кг/м2 соотношение шага к сечению составляет 75/100 мм. Вообще, чем больше сечение балок, тем больше расстояние между ними.
Применяя калькулятор для определения сечения, необходимо пользоваться справочными материалами для более точных результатов.
Кроме полученных точных результатов, прочность конструкции зависит от качества материала.
Заготовки используют из хвойных пород дерева, влажностью до 14%. Древесина не должна быть поражена грибком и насекомыми. Ну а чтобы увеличить срок эксплуатации деревянной конструкции, заготовки перед монтажом необходимо обрабатывать антисептиком.
В следующем видео можно понаблюдать пример работы в программе для расчетов перекрытий.
Что еще почитать по теме?
Автор статьи:
Сергей Новожилов — эксперт по кровельным материалам с 9-летним опытом практической работы в области инженерных решений в строительстве.
Понравилась статья? Поделись с друзьями в социальных сетях:
Вконтакте
Одноклассники
Google+
Расчет индивидуальной железобетонной балки
При возведении зданий и сооружений для устройства перекрытий и стеновой кладки над различными проемами часто, помимо применения железобетонных балок и перемычек заводского изготовления, возникает необходимость в устройстве индивидуальных монолитных железобетонных балок непосредственно на строительной площадке.
Что касается строительства с применением несъемной опалубки, то индивидуальные балки являются его неотъемлемой структурной частью. При наличии конструкторской проектной документации вопросов по их устройству не возникает.
Но на площадках индивидуальных застройщиков весьма распространена практика строительства по архитектурным проектам, так называемым эскизникам, и расчеты монолитных балок приходится выполнять по ходу строительства.
Разберем, как можно выполнить расчет железобетонной балки самостоятельно.
Что принять за основу расчета (общие рекомендации)
Основными нормативами для расчетов железобетонных конструкций являются методики, изложенные в Пособиях к СНиП 2.03.01-84 и СП 52-101-2003.
Конечно, правильнее применять более «свежие» методики, но, судя по отзывам специалистов, для людей, решивших самостоятельно разобраться и рассчитать вручную железобетонную конструкцию, не имея предварительного опыта и специального образования, проще воспользоваться старой методикой.
При этом нужно учесть, что весь расчет следует выполнять в рамках одних нормативов. Если уж начали рассчитывать по новому, значит, во всем применяйте данные нового СП.
Для примера, как они могут различаться, приведем таблицы расчетных значений сопротивления бетона сжатию:
Расчетные значения сопротивления бетона сжатию (СНиП 2.03.01-84*(1996))
Расчетные значения сопротивления бетона сжатию (СП 52-101-2003)
Разница очевидна и по выбору типа бетона, и по количеству расчетных значений.
В дополнение приведем соответствие классов бетона по СНиП 2.03.01-84 маркам бетона по СНиП II-21-75, все еще используемым в обиходе (соответствие — по столбцам):
Марки бетона (СНиП II-21-75)
| М50 | М75М100 | — | М150 | — | М200М250 | М300 | М350 | М400М450 | М500 | М600 | М700 | — | М800 |
Классы бетона (СНиП 2.03.01-84)
| В3,5 | В5 | В7,5 | В10 | В12,5 | В15 | В20 | В25 | В30 | В35 | В40 | В45 | В50 | В55 | В60 |
Железобетон – материал, включающий в себя несколько составляющих, поэтому учесть работу каждого элемента в общей структуре балки (под влиянием всех факторов на ее несущую способность) весьма затруднительно и под силу лишь профессионалам, которые имеют опыт практических расчетов на основе сопромата.
Конечно, существуют специальные расчетные программы, но они весьма не дёшевы и имеют их крупные проектные организации. Для единичного же расчета углубляться в изучение этих программных комплексов нет особой целесообразности.
На помощь может прийти универсальная программа расчета железобетонной балки. Ее работа основана на автоматическом расчете основных параметров при введении исходных данных, таких как: длина перекрываемого пролета, тип железобетонной опоры, значения нагрузок и прочее.
Область применения бетонных блоков для стен подвалов довольно обширна. Кроме возведения ленточного фундамента, они применяются при строительстве технических подпольев и стен цокольных этажей, используются для обнесения опасных участков дорог, а также при постройке гаражей.
При строительстве любых сооружений и зданий основным из требований к конструкции является надежность, должное сопротивление деформированию во время воздействия различных нагрузок. О железобетонных балках перекрытия читайте здесь.
Встроенный в программу калькулятор бетонной балки определит количество арматуры, в зависимости от заданного диаметра стержней и сечения.
Ориентирами же могут служить следующие базовые положения:
- Вся арматура в железобетонной конструкции должна располагаться внутри бетона не ближе 2см от его поверхности
- Арматура должна работать на растяжение, поэтому устанавливать её следует в нижней части конструкции. В верхнем поясе рабочие арматурные стержни устанавливают в случаях, отдельного изготовления балки на строительной площадке с последующим подъемом краном для установки её в проектное положение
- Диаметр сечения рабочей (продольной) арматуры принимается не менее 12мм и класс её – АIII
- Высота сечения не менее(!) 1/20 части перекрываемого пролета (6м/20 = 0,3м)
- Значение отношения высоты к ширине от 2 до 4 (h/b = 2~4)
Также калькулятор железобетонной балки способен выполнить расчет на прочность и рассчитать прогиб.
Определение типа опирания балки
В зависимости от типа опирания (см. Устройство буронабивных свай) выбирается метод расчета. Рассмотрим основные типы опор железобетонных балок на несущие конструкции.
Шарнирный тип опирания.
Таковым считается случай, когда в проектное положение устанавливают предварительно изготовленную железобетонную балку.
Причем конструкцией не предусмотрены никакие закладные детали для последующего жесткого соединения с конструктивными элементами здания. Как правило при таком типе опирания ширина плоскости опирания на несущие конструкции (стены, колонны) не превышает 20см.
Жестко защемленная балка.
Чтобы считать балку жестко защемленной на концах, условия должны быть следующими: балка бетонируется одновременно с прилегающими конструкциями в составе монолитной стены, в ее конструкции имеются закладные детали для последующего жесткого соединения с остальными конструктивными элементами.
При бетонировании создает монолитные узлы соединений конструкций.
Многопролетное опирание.
При необходимости перекрыть несколько последовательно расположенных пролетов опирание балки выполняется на несколько опорных конструкций (колонны, простенки между окон).
Такое опирание рассчитывается как многопролетное в случае, если опоры шарнирные). Если опоры жесткие, то расчет ведется по каждому отдельному пролету, как по самостоятельной балке.
Консольное опирание.
Речь о таком типе опирания ведется, когда один или оба конца балки не имеют опор, а так же при отступе опор от концов на некоторое расстояние (свес с опоры).
Например: часть плиты перекрытия выпущена за пределы стены в виде козырька. Такую плиту можно рассматривать балкой с консольной опорой.
Нагрузки на балку
Еще из курса физики известно: все, что неподвижно закреплено (прибито, приклеено и пр.) на чём-либо – это статическая нагрузка.
Соответственно, движущиеся (прыгающие, сотрясающие и т.п.) объекты создают динамические нагрузки.
Но в свою очередь эти нагрузки в случае строительной физики подразделяются на сосредоточенные и равномерные. К сосредоточенным нагрузкам можно отнести, к примеру, бетонную скульптуру, установленную на перемычке (балке) арки.
С равномерными нагрузками несколько сложнее, так как они подразделяются еще на подгруппы: равномерно распределенные по всей поверхности, равномерно изменяющиеся по длине или ширине и неравномерно изменяющейся, соответственно.
Для сосредоточенной нагрузки единицей измерения принят килограмм (килограмм-сила (кгс), ньютон (Н)).
Единицей измерения для распределенной нагрузки принято отношение кгс/м?, однако, при расчетах сборных железобетонных балок для перекрытия значение распределенной нагрузки принимается на метр погонный (м.п.). Для построения эпюр изгибающих моментов к расчету принимается только длина, а высота и ширина игнорируются.
Чтобы перейти от метров квадратных к погонным, когда идет расчёт балки перекрытия, значение распределенной нагрузки умножим на показатель расстояния между балками перекрытия (их осями).
А если определяем нагрузку на перемычку, то плотность лежащего на перемычке материала конструкции, умножаем на ширину и высоту этой конструкции.
Арматура для изготовления стропильных и подстропильных железобетонных балок должна быть предварительно напряженной, для отдельных типов допускаются исключения предусмотренные ГОСТом.
При изготовлении железобетонных конструкций, плотность укладки бетона контролируют по коэффициенту уплотнения (отношение действительной плотности бетона к ее расчетному значению). О данном виде изделий читайте в этой статье.
От тщательности сбора и расчета нагрузок на балку зависит конструктивная надежность сооружения.
Но если со статическими нагрузками все более-менее ясно, то рассчитать возможные динамические нагрузки на все случаи жизни – занятие неблагодарное и приведет к малообоснованному удорожанию строительства.
Поэтому динамические нагрузки принимаются с различными коэффициентами, приближающими к реалиям возможности возникновения одномоментно различных динамических воздействий в данном конкретном месте.
Приведем некоторые значения, наиболее часто учитываемых при расчетах, нагрузок:
- Вес сборных железобетонных плит заводского изготовления (h=220 мм) 310 ~ 350кг/м2;
Объемный вес бетона М200 — 2450 кг/м3; - Полезная нагрузка на перекрытие с учетом различных коэффициентов:
жилые помещения ~200 кг/м2
офисные помещения ~ 250 кг/м2 - Вес покрытия пола из керамической плитки с цементно-песчаной стяжкой толщиной 25-30мм ~ 100 кг/м2
- Снеговые, дождевые, сейсмические и прочие нагрузки от природных факторов нужно принимать по СНиП 23-01-99*(«Строительная климатология») с учетом климатического района строительства.
Таким образом, выполнить расчет железобетонной балки вручную вполне возможно, но, на наш взгляд, гораздо рациональнее будет потрачено время, если воспользоваться какой-либо программой для расчета.
Мне нравится3Не нравится
Бесплатный калькулятор луча | Калькулятор изгибающего момента, поперечной силы и прогиба
Добро пожаловать в наш бесплатный онлайн-калькулятор диаграмм изгибающего момента и поперечной силы, который может генерировать диаграммы реакций, поперечных сил (SFD) и изгибающих моментов (BMD) консольной балки или просто поддерживаемой балки. Используйте этот калькулятор пролета балки, чтобы определить реакции на опоры, построить диаграмму сдвига и момента для балки и рассчитать прогиб стальной или деревянной балки. Бесплатный онлайн-калькулятор балки для создания реакций, расчета прогиба стальной или деревянной балки, построения диаграмм сдвига и момента балки.Это бесплатная версия нашего полного программного обеспечения SkyCiv Beam. Доступ к нему можно получить из любой из наших Платных учетных записей, которая также включает полное программное обеспечение для структурного анализа.
Используйте интерактивное окно выше, чтобы просмотреть и удалить длину балки, опоры и добавленные нагрузки. Любые внесенные изменения автоматически перерисовывают диаграмму свободного тела для любой балки с опорой или консольной балкой. Калькулятор реакции балки и расчет изгибающего момента запускаются после нажатия кнопки «Решить» и автоматически генерируют диаграммы сдвига и изгибающего момента.Вы также можете щелкнуть отдельные элементы этого калькулятора балки LVL, чтобы редактировать модель.
Калькулятор пролета балки легко рассчитает реакции на опорах. Он может рассчитывать реакции на опорах консольных или простых балок. Это включает в себя расчет реакций для консольной балки, которая имеет реакцию изгибающего момента, а также силы реакции x, y.
Вышеупомянутый калькулятор пролета стальной балки — это универсальный инструмент для проектирования конструкций, используемый для расчета изгибающего момента в алюминиевой, деревянной или стальной балке.Его также можно использовать в качестве калькулятора несущей способности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Он способен выдерживать до 2 различных сосредоточенных точечных нагрузок, 2 распределенных нагрузки и 2 момента. Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками (UDL), треугольными распределенными нагрузками или трапециевидными распределенными нагрузками. Все нагрузки и моменты могут быть направленными как вверх, так и вниз по величине, что должно учитывать наиболее распространенные ситуации анализа балок.Расчет изгибающего момента и поперечной силы может занять до 10 секунд, и обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, диаграммой поперечной силы и диаграммой изгибающего момента балки.
Одна из самых мощных функций — использование его в качестве калькулятора отклонения балки (или калькулятора смещения балки). Это можно использовать для наблюдения расчетного прогиба балки с опорой или консольной балки. Возможность добавлять формы сечения и материалы делает его полезным в качестве калькулятора деревянных балок или в качестве калькулятора стальных балок для проектирования балок lvl или i.На данный момент эта функция доступна в SkyCiv Beam, который имеет гораздо больше функций для проектирования деревянных, бетонных и стальных балок.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облачных вычислений. Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и совершенствовать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Размеры стальной балки
| SkyCiv
Наличие хорошего ресурса для размеров двутавровых балок очень важно при проектировании конструкций.Для нас, как инженера-строителя, важно определить секции, которые не только безопасны, но и рентабельны. С помощью приведенной ниже таблицы размеров стальных балок SkyCiv стремится получить бесплатный ресурс, к которому можно будет получить доступ в любое время через браузер. Приведенная ниже таблица размеров стальных балок поможет инженерам-строителям найти подходящий размер и форму, которые вам нужны для вашего проекта. Эти свойства важны при проверке прочности секции, что является само определение конструкции конструкции.
Таблица размеров стальных балок — это интерактивная таблица, в которой перечислены размерные и геометрические свойства сечения. Эти свойства могут помочь инженерам найти желаемый стальной профиль, который они ищут. Просто выберите систему единиц измерения, библиотеку, прежде чем выбирать форму, чтобы отобразить размеры балки этой формы. Библиотека содержит разделы из Австралии, США, Канады, Великобритании и Европы. Программное обеспечение извлекает размеры балки непосредственно из базы данных Structural 3D, которая является основным программным обеспечением для трехмерного структурного анализа платформы SkyCiv, которое также доступно для использования в веб-браузере.Эта информация обычно требует, чтобы пользователь держал под рукой ручные схемы или схемы стальных балок, что может доставлять неудобства, т. Е. Если у пользователя есть копия. Хотя приобретение руководства по стали требует денежных затрат, мы должны еще раз подчеркнуть, что справочная таблица SkyCiv легко доступна здесь бесплатно.
Некоторые из размеров, которые может отображать этот инструмент:
- Размеры двутавровой балки
- Размеры S-образной балки
- Квадрат полый / HSS Размеры
- Круглые размеры из быстрорежущей стали
- Ширина балки с широким фланцем Размеры
- Т-образная балка Размеры
- Размеры каналов
- Размеры уголков
- Имперские и метрические размеры балки
Приведенные выше размеры стальных секций должны дать пользователю возможность легко получить доступ к свойствам элементов и размерам часто используемых секций в различных библиотеках по всему миру.Мы надеемся, что инженеры найдут ссылки на эти размеры и размеры стальных балок, которые будут полезны для их работы. Опять же, в настоящее время существуют размеры и размеры стали для профилей из Австралии, США, Великобритании, Европы и Канады. Если конкретная библиотека, которую вы используете, недоступна, вы можете связаться с нами здесь. Мы открыты для улучшения и расширения нашей базы данных. Еще одним замечательным аспектом этого инструмента является то, что он может преобразовывать размеры балки из метрических в британские и наоборот. Это экономит время инженера при работе с единичными системами и снижает риск ошибки в расчетах.
Свойства сечения, отображаемые в приведенной выше таблице, включая площадь поперечного сечения (A), полярный момент инерции (J), момент площади (Iz, Iy), модуль сечения и постоянную деформации (Iw). Эти результаты чрезвычайно важны при выборе конструкционной стали для конструкций балок и колонн. Это свойства, которые контролируют количество и тип силы, которую может принять стальной элемент.
Здесь, в SkyCiv, у нас есть ряд программного обеспечения (бесплатного и платного), которое позволяет инженерам моделировать и проектировать свои конструкции.Наш калькулятор свободных балок — это простой в использовании калькулятор, который помогает анализировать консольные балки и балки с простой опорой. Вы также можете воспользоваться нашим калькулятором ферм для быстрого анализа 2D ферм. Для небольших 2D-рам вы можете воспользоваться нашим бесплатным калькулятором несущих рам. Для типичных форм нестандартных размеров стали калькулятор свободного момента инерции является хорошим средством для определения их геометрических характеристик и характеристик сечения.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облачных вычислений.Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и совершенствовать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Расчет луча
| MechaniCalc
Калькулятор балки позволяет анализировать напряжения и прогибы в прямых балках.
Опции
Пример загрузки
Очистить все данные
Входы
Введите данные балки, затем нажмите кнопку «Рассчитать результаты»:
—
Добавить ограничение
Удалить ограничение
Невозможно отобразить сюжет — браузер устарел.
Рассчитать результаты
Предупреждение — Перед решением необходимо исправить следующее:
Дисплейные блоки
Результаты
Результаты анализа пучка подробно описаны ниже. Задача решалась в виде конечно-элементной модели с использованием балочных элементов. Для получения дополнительной информации о том, как были получены эти результаты, обратитесь к справочнику по конечно-элементному анализу и справочнику по напряжению и прогибу балки.
Обзор результатов
Максимальный прогиб и наклон приведены ниже:
| Значение | Расположение | |
|---|---|---|
| Максимальное отклонение: | ||
| Максимальный наклон: |
Схема свободного тела (FBD) и деформированная сетка показаны ниже.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
См. Полную информацию о результатах на других вкладках (выше).
Обзор модели
Модель с приложенными силами и ограничениями показана ниже:
Невозможно отобразить сюжет — браузер устарел.
Свойства материала
Материал:
| Имущество | Значение |
|---|---|
| Предел текучести | |
| Максимальная прочность | |
| Модуль упругости | |
| Коэффициент Пуассона |
Свойства поперечного сечения
Поперечное сечение:
| Имущество | Значение |
|---|---|
| Высота (Y) | |
| Ширина (X) | |
| Толщина полотна | |
| Толщина фланца | |
| Площадь | |
| Центроидное расстояние (в направлении первичного изгиба) | |
| Момент инерции, центроидный (относительно оси первичного изгиба) |
Диаграмма момента сдвига
Диаграммы сдвига и момента показаны ниже.Соблюдаются стандартные условные обозначения для диаграмм момента сдвига:
- Сдвиг: положительный сдвиг вызывает вращение балки по часовой стрелке, отрицательный сдвиг вызывает вращение против часовой стрелки.
- Момент: Положительный момент сжимает верхнюю часть балки и удлиняет нижнюю часть балки (т.е. заставляет балку «улыбаться»).
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Графики напряжений
Графики напряжений показаны ниже.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Напряжения рассчитываются на основе следующих уравнений:
| Осевое напряжение | Напряжение сдвига | Напряжение изгиба | Напряжение по Мизесу |
|---|---|---|---|
Графики прогиба
Графики прогиба показаны ниже.Условные обозначения прогибов:
.
- X: положительный направо, отрицательный налево
- Y: положительный вверх, отрицательный вниз
- Наклон: линейка правой руки (положительное значение против часовой стрелки, отрицательное по часовой стрелке)
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Эта проблема была решена в виде конечно-элементной модели. На этой вкладке представлены результаты для отдельных узлов и элементов модели.
На приведенном ниже графике показана сетка с номерами элементов , помеченными:
Невозможно отобразить сюжет — браузер устарел.
Узловые результаты
Ниже приведены результаты для каждого узла. Следует отметить несколько моментов:
- Определенные узлы связаны с точками, и для этих узлов указывается номер связанной точки.
- Сначала перечислены все узлы, связанные с точками, за ними следуют узлы, созданные как часть процесса построения сетки.
- Для ограниченных степеней свободы могут существовать внешние реакции. Любые узлы, не имеющие ограничений, не будут иметь внешних реакций.
Элементарные результаты
Ниже приведены результаты для каждого элемента. Следует отметить несколько моментов:
- Каждый элемент состоит из 2 узлов. В таблице эти узлы обозначаются как «Узел 1» и «Узел 2».
- Внутренние реакции даны в терминах глобальной системы координат (т.е. X и Y), а также в локальной системе координат (т.е. «осевой» вдоль оси элемента, «сдвиг» перпендикулярно элементу).
Загрузить результаты в Excel
Загрузите файл Excel на свой компьютер, содержащий узловые и элементарные результаты.
Скачать отчет
Сохраните отформатированный документ Word на свой компьютер с подробным описанием входных данных и результатов анализа.
Скачать входной файл
Сохранить все входные данные в файл. Позже вы можете загрузить этот файл, чтобы продолжить с того места, где вы остановились.
Требуется больше функциональности?
Зарегистрируйтесь, чтобы получить полный доступ ко всем калькуляторам и другому контенту. Типы подписки описаны ниже вместе с преимуществами каждого из них.
- Цена
- Доступ к калькуляторам
- Логин
- Создание материалов
- Создание сечений
- Сохранение файлов
- Отчетность
39 долларов США.99 / месяц 249,99 долларов США в год Полный
Полный Доступ к калькуляторам
Плавающие лицензии
Плавающие лицензии
- Учить больше »
- Зарегистрироваться сейчас
Просто поддерживаемый калькулятор пучка | calcresource
Предпосылки
Оглавление
Введение
Балка с простой опорой — одна из самых простых конструкций.У него всего две опоры, по одной с каждой стороны. Одна штифтовая опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободное вращение вокруг них. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя свободному горизонтальному перемещению препятствует другая опора.
Удаление любой из опор или установка внутреннего шарнира приведет к тому, что балка с простой опорой перейдет в механизм, то есть тело перемещается без ограничений в одном или нескольких направлениях.Очевидно, это нежелательно для несущей конструкции. Следовательно, балка с простой опорой не обеспечивает избыточности с точки зрения опор. Если произойдет локальный сбой, вся конструкция рухнет. Эти типы структур, которые не предлагают избыточности, называются критическими или детерминантными структурами . Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией .
Допущения
Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов. Как правило, для плоской конструкции с плоской нагрузкой интересующими внутренними воздействиями являются осевая сила N, поперечная сила сдвига V и изгибающий момент M. Для балки с простой опорой, которая несет только поперечные нагрузки, осевая сила всегда равна ноль, поэтому им часто пренебрегают. Результаты расчетов на странице основаны на следующих предположениях:
- Материал однороден и изотропен (другими словами, его характеристики одинаковы во всех точках и в любом направлении)
- Материал линейно эластичный
- Нагрузки прикладываются статично (они не меняются со временем)
- Поперечное сечение одинаково по всей длине балки
- Прогибы небольшие
- Каждое поперечное сечение, которое изначально является плоским, а также перпендикулярно продольной оси, остается плоской и перпендикулярно отклоненной оси.Это тот случай, когда высота поперечного сечения намного меньше длины балки (в 10 и более раз), а также поперечное сечение не является многослойным (не сечение сэндвич-типа).
Последние два предположения удовлетворяют кинематическим требованиям теории пучка Эйлера-Бернулли, которая здесь также принята.
Условные обозначения
Для расчета внутренних сил и моментов при любом разрезе сечения балки необходимо условное обозначение. Здесь приняты следующие значения:
- Осевая сила считается положительной, когда она вызывает натяжение детали.
- Сдвигающая сила положительна, когда она вызывает вращение детали по часовой стрелке.
- Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.
Эти правила хотя и не являются обязательными, но достаточно универсальны. Другой набор правил, если его последовательно соблюдать, также даст те же физические результаты.
Символы
- E: модуль упругости материала (модуль Юнга)
- I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
- L: общий пролет балки
- R: опора реакция
- d: прогиб
- M: изгибающий момент
- V: поперечная поперечная сила
- \ theta: slope
Балка с простой опорой и равномерно распределенной нагрузкой
Нагрузка w распределяется по всему пролету балки с постоянной величиной и направление. 3)} {24 EI} 90 612
Балка с простой опорой и точечной силой в середине
Сила сосредоточена в одной точке, расположенной в середине балки.Однако на практике сила может распространяться на небольшую площадь, хотя размеры этой области должны быть существенно меньше длины пролета балки. В непосредственной близости от приложения силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным. Однако это только местное явление. По мере удаления от места расположения силы результаты становятся действительными в силу принципа Сен-Венана.
В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенной точечной силы P, приложенной в середине.2)} {16 E I} &, x> L / 2 \ end {align} \ right.
где:
\ строго {x} = L-x
Балка с простой опорой и точечной силой в произвольном положении
Сила сосредоточена в одной точке в любом месте пролета балки. Однако на практике сила может распространяться на небольшую площадь. Однако, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки.В непосредственной близости от силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным. Однако это только локальное явление, и по мере удаления от места расположения силы расхождение результатов становится незначительным.
В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенной точечной силы P, приложенной на случайном расстоянии a от левого конца.
Балка с точечной нагрузкой в произвольном положении | |
|---|---|
| Количество | Формула |
| Реакции: | R_A = {Pb \ over L} R_B = {Pa \ над L} |
| Концевые уклоны: | \ theta_A = — \ frac {P b (L ^ 2-b ^ 2)} {6E IL} \ theta_B = \ frac {P a (L ^ 2-a ^ 2)} {6E IL} |
| Предельный изгибающий момент: | M_u = {Pab \ over L} |
| Предельное усилие сдвига: | V_u = \ left \ {\ begin {выровнено } & {Pb \ over L} &, \ textrm {if:} a \ le L / 2 \\ — & {Pa \ over L} &, \ textrm {if:} a> L / 2 \ end {выровнено} \верно. 2 )} {6E IL} |
| Предельный изгибающий момент: | M_u = \ left \ {\ begin {align} & {Mb \ over L} &, \ textrm {if:} a \ le L / 2 \ \ — & {Ma \ over L} &, \ textrm {if:} a> L / 2 \ end {align} \ right.2} {2 E I} &, x> a \ end {align} \ right. |
где: b = La \ строго {x} = Lx | |
Балка с простой опорой и треугольной нагрузкой
Нагрузка распределяется по всему пролету балки, однако ее величина не константа, но изменяется линейно, начиная от нуля на левом конце до своего пикового значения w_1 на правом конце. Размеры w_1 — сила на длину. Общее количество силы, приложенной к балке, равно W = {1 \ over2} w L, где L — длина пролета.
Ориентация треугольной нагрузки важна! Формулы, представленные в этом разделе, были подготовлены для случая восходящей нагрузки (слева направо), как показано на схеме. Для нисходящей нагрузки вы можете отразить балку так, чтобы ее левый конец (точка A) был наименее загруженным. Ось x и все результаты также будут отражены.
В следующей таблице представлены формулы, описывающие статический отклик простой балки при линейно изменяющейся (треугольной) распределенной нагрузке, восходящей слева направо.4} {24EIL}
где:
C = \ sqrt {15- \ sqrt {120}} \ left (\ sqrt {15} + \ sqrt {50} \ right) \ приблизительно 22.01237
Балка с простой опорой и трапецеидальной нагрузкой
Нагрузка распределяется по всему пролету балки и имеет линейно изменяющуюся величину, начиная с w_1 на левом конце и заканчивая w_2 на правом конце. Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, равно W = {L \ over2} (w_1 + w_2), где L — длина пролета.
Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба). 3} {24EI}
где:
w_x = w_1 + {(w_2-w_1) x \ over L}
901 03
Балка с простой опорой и трапециевидным распределением нагрузки типа плиты
Такое распределение нагрузки типично для балок по периметру плиты.Распределение имеет трапециевидную форму с максимальной величиной w внутри балки, а на двух ее концах становится равной нулю. Размеры (\ w \) — сила на длину. Общее количество силы, приложенной к балке, равно W = w (La / 2-b / 2), где L — длина пролета, а a, b — длины с левой и правой стороны балки соответственно, где распределение нагрузки равно разная (треугольная).
В следующей таблице представлены формулы, описывающие статический отклик простой балки при трапецеидальном распределении нагрузки, как показано на схеме выше.3
Балка с простой опорой и частично распределенной равномерной нагрузкой
Нагрузка распределяется на часть пролета балки с постоянной величиной w, в то время как оставшийся пролет разгружен. Размеры w — сила на длину. Общее количество силы, приложенной к балке, равно W = \ left (L-a-b \ right) w, где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки, соответственно.
В следующей таблице представлены формулы, описывающие статический отклик простой балки при частично распределенной равномерной нагрузке.2} {2 E I} &, x \ ge L-b \ end {align} \ right.
где:
\ острый {x} = Lx
x_a = xa
L_w = Lab
Балка с простой опорой и частично распределенной трапециевидной нагрузкой
Нагрузка распределяется на часть пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет не нагружен. Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, равно W = {L-a-b \ over2} (w_1 + w_2), где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки соответственно.
Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).
Это самый общий случай. Формулы для частично распределенных равномерных и треугольных нагрузок можно получить, соответствующим образом задав значения w_1 и w_2. Кроме того, соответствующие случаи для полностью нагруженного пролета можно получить, установив a и b равными нулю.
В следующей таблице представлены формулы, описывающие статический отклик простой балки при частично распределенной трапециевидной нагрузке.3
Статьи по теме
Понравилась эта страница? Поделись с друзьями!
Балки — поддерживаются на обоих концах
Напряжение в изгибаемой балке можно выразить как
σ = y M / I (1)
, где
σ = напряжение (Па (Н / м) 2 ), Н / мм 2 , psi)
y = расстояние до точки от нейтральной оси (м, мм, дюйм)
M = изгибающий момент (Нм, фунт дюйм)
I = момент инерции (м 4 , мм 4 , в 4 )
Калькулятор ниже можно использовать для расчета максимального напряжения и прогиба балок с одной одиночной или равномерно распределенной нагрузкой.
Балка, поддерживаемая на обоих концах — равномерная непрерывная распределенная нагрузка
Момент в балке с равномерной нагрузкой, поддерживаемой на обоих концах в положении x, может быть выражен как
M x = qx (L — x) / 2 (2)
где
M x = момент в положении x (Нм, фунт дюйм)
x = расстояние от конца (м, мм, дюйм)
Максимум момент находится в центре балки на расстоянии L / 2 и может быть выражен как
M max = q L 2 /8 (2a)
где
M max = максимальный момент ( Нм, фунт-дюйм)
q = равномерная нагрузка на единицу длины балки (Н / м, Н / мм, фунт / дюйм)
9133 2 L = длина балки (м, мм, дюйм)
Максимальное напряжение
Уравнения 1 и 2a могут быть объединены для выражения максимального напряжения в балке с равномерной нагрузкой. на обоих концах на расстоянии L / 2 как
σ max = y max q L 2 / (8 I) (2b)
где
σ max = максимальное напряжение (Па (Н / м 2 ), Н / мм 2 , psi)
y max = расстояние до крайней точки от нейтральной оси (м, мм, дюйм)
- 1 Н / м 2 = 1×10 -6 Н / мм 2 = 1 Па = 1.4504×10 -4 фунт / кв. Дюйм
- 1 фунт / дюйм (фунт / дюйм 2 ) = 144 фунт / кв. Дюйм (фунт на / фут 2 ) = 6894,8 Па (Н / м 2 ) = 6,895×10 — 3 Н / мм 2
Максимальный прогиб :
δ max = 5 q L 4 / (384 EI) (2c)
где
375 375 90 max = максимальный прогиб (м, мм, дюйм)
E = Модуль упругости (Па (Н / м 2 ), Н / мм 2 , psi)
Прогиб в положении x:
δ x = qx ( L 3 — 2 L x 2 + x 3 ) / (24 EI) (2d)
Примечание! — прогиб часто является ограничивающим фактором при проектировании балки.Для некоторых применений балки должны быть прочнее, чем требуется при максимальных нагрузках, чтобы избежать недопустимого прогиба.
Силы, действующие на концы:
R 1 = R 2
= q L / 2 (2e)
где
R = сила реакции (Н, фунт)
Пример — балка с равномерной нагрузкой, метрические единицы
Балка UB 305 x 127 x 42 длиной 5000 мм несет равномерную нагрузку 6 Н / мм .Момент инерции балки составляет 8196 см 4 (81960000 мм 4 ) , а модуль упругости стали, использованной в балке, составляет 200 ГПа (200000 Н / мм 2 ) . Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).
Максимальное напряжение в балке можно рассчитать
σ max = (150 мм) (6 Н / мм) (5000 мм) 2 / (8 (81960000 мм 4 ))
= 34.3 Н / мм 2
= 34,3 10 6 Н / м 2 (Па)
= 34,3 МПа
Максимальный прогиб балки можно рассчитать
δ макс = 5 (6 Н / мм) (5000 мм) 4 / (( 200000 Н / мм 2 ) ( 81960000 мм 4 ) 384)
= 2,98 мм
Калькулятор балки с равномерной нагрузкой — метрические единицы
- 1 мм 4 = 10 -4 см 4 = 10 -12 м 30 4 0 4 90 1 см 4 = 10 -8 м = 10 4 мм
- 1 дюйм 4 = 4.16×10 5 мм 4 = 41,6 см 4
- 1 Н / мм 2 = 10 6 Н / м 2 (Па)
Расчет балки равномерной нагрузки — Британские единицы
Пример — балка с равномерной нагрузкой, британские единицы
Максимальное напряжение в стальной широкополочной балке W 12 x 35 дюймов, 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 2
00 psi
, при равномерной нагрузке 100 фунтов / дюйм можно рассчитать как
σ max = y max q L 2 / (8 I)
= (6.25 дюймов (100 фунтов / дюйм) (100 дюймов) 2 / (8 (285 дюймов 4 ))
= 2741 (фунт / дюйм 2 , psi)
Максимальное отклонение может можно рассчитать как
δ max = 5 q L 4 / (EI 384)
= 5 (100 фунтов / дюйм) (100 дюймов) 4 / ((2
00 фунтов / дюйм
2 ) (285 дюймов 4 ) 384)
= 0,016 дюйма
Балка, поддерживаемая на обоих концах — нагрузка в центре
Максимальный момент в балке с центральной нагрузкой, поддерживаемой с обоих концов :
M max = FL / 4 (3a)
Максимальное напряжение
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой с обоих концов:
σ max = y max FL / (4 I) (3b) 901 30
, где
F = нагрузка (Н, фунт)
Максимальный прогиб можно выразить как
δ max = FL 3 / (48 EI) (3c)
Силы, действующие на концы:
R 1 = R 2
= F / 2 (3d)
Калькулятор балки с одним центром нагрузки — метрические единицы
Калькулятор балки с одним центром нагрузки — британская система мер Единицы
Пример — балка с одной центральной нагрузкой
Максимальное напряжение в стальной широкополочной балке шириной 12 x 35 дюймов, 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 2
00 psi
, с центральной нагрузкой 10000 фунтов можно рассчитать как
σ max = y max FL / (4 I)
= (6.25 дюймов) (10000 фунтов) (100 дюймов) / (4 (285 дюймов 4 ))
= 5482 (фунт / дюйм 2 , фунт / кв. Дюйм)
Максимальный прогиб можно рассчитать как
δ макс = FL 3 / EI 48
= (10000 фунтов / дюйм) (100 дюймов) 3 / ((2
00 фунтов / дюйм
2 ) (285 дюймов 4 ) 48 )
= 0,025 дюйма
Некоторые типичные пределы отклонения по вертикали
- Полное отклонение: пролет / 250
- отклонение при динамической нагрузке: пролет / 360
- консоли: пролет / 180
- балки деревянных перекрытий в домашних условиях: пролет / 330 (макс. 14 мм)
- хрупкие элементы: пролет / 500
- подкрановые балки: пролет / 600
Балка, поддерживаемая на обоих концах — эксцентричная нагрузка
Максимальный момент в балке с одиночной эксцентричной нагрузкой в точке нагрузки:
M макс = F ab / L (4a)
Максимальное напряжение
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой с обоих концов:
σ max = y max F ab / (LI) (4b)
Максимальный прогиб в точке нагрузки можно выразить как
δ F = F a 2 b 2 / (3 EIL) (4c)
Силы, действующие на торцы:
R 1 = F b / L (4d)
R 2 = F a / L (4e)
Балка, поддерживаемая на обоих концах — две эксцентрические нагрузки
Максимальный момент (между нагрузками) в балке с двумя эксцентрическими нагрузками:
M max = F a (5a)
Максимальное напряжение
Максимальное напряжение в балке с двумя эксцентрическими нагрузками, поддерживаемыми на обоих концах:
σ max = y max F a / I (5b)
Максимум прогиб в точке нагрузки можно выразить как
δ F = F a (3L 2 — 4 a 2 ) / (24 EI) (5c)
Силы, действующие на торцы:
R 1 = R 2
= F (5d)
Вставьте балки в свою модель Sketchup с помощью Engineering ToolBox Sketchup Extension
Балка поддерживается на обоих концах — трехточечная нагрузка
Максимальный момент (между нагрузками) в балке с тремя точечными нагрузками:
M max 91 376 = FL / 2 (6a)
Максимальное напряжение
Максимальное напряжение в балке с тремя точечными нагрузками, поддерживаемыми с обоих концов:
σ max = y max FL / (2 I) ( 6b)
Максимальный прогиб в центре балки можно выразить как
δ F = FL 3 / (20.22 EI) (6c)
Силы, действующие на концах:
девяносто одна тысяча триста тридцать два R + 1 + = R 2
= 1,5 F (6d)
Beam Грузы — Поддержка Калькулятор Силы
Калькулятор Интернет Поддержка Force Beam
Калькулятор ниже может быть использована для расчета сил поддержки — R 1 и R 2 — для балок до 6 асимметрично нагрузок.
Длина балки (м, фут)
Сила F1 (Н, фунт f ) расстояние от R 1 (м, фут)
Сила F2 (Н, фунт f ) расстояние от R 1 (м, фут)
Сила F3 (Н, фунт f ) расстояние от R 1 (м, фут)
Сила F4 ( Н, фунт f ) расстояние от R 1 (м, фут)
Сила F5 (Н, фунт f ) расстояние от R 1 (м, фут)
Сила F6 (Н, фунт f ) расстояние от R 1 (м, фут)
Для балансирующей балки, нагруженной грузами (или другими силами нагрузки), силы реакции — R — на опорах равно , сила нагрузки — F . Баланс сил может быть выражен как
F 1 + F 2 + …. + F n = 1 + R 2 (1)
где
F = усилие от нагрузки (Н, фунт f )
R = сила от опоры (Н, фунт f )
Дополнительно для балки в балансе алгебраическая сумма моментов равно нулю .Баланс момента может быть выражен как
F 1 a f1 + F 2 a f2 + …. + F n a fn = R a r1 + R a r2 (2)
где
a = расстояние от силы до общей точки отсчета — обычно расстояние до одной из опор (м, футы)
Пример — A балка с двумя симметричными нагрузками
Длинная балка 10 м с двумя опорами нагружена двумя равными и симметричными нагрузками F 1 и F 2 , каждая по 500 кг .Опорные силы F 3 и F 4 могут быть рассчитаны
(500 кг) (9,81 м / с 2 ) + (500 кг) (9,81 м / с 2 ) = R 1 + R 2
=>
R 1 + R 2 = 9810 N
= 9,8 кН
Примечание! Нагрузка от веса груза — м — мг Ньютон — где г = 9.81 м / с 2 .
При симметричных и равных нагрузках опорные силы также будут симметричными и равными. Используя
R 1 = R 2
, приведенное выше уравнение можно упростить до
R 1 = R = (9810 N) / 2 =
4905 N
= 4,9 кН
Связанные мобильные приложения из Engineering ToolBox
— бесплатные приложения для автономного использования на мобильных устройствах.
Пример — Балка с двумя несимметричными нагрузками
A 10 м длинная балка с двумя опорами нагружена двумя нагрузками, 500 кг расположен 1 м от конца ( R 1 ) , а другой груз 1000 кг расположен 6 м с того же конца. Баланс сил можно выразить как
(500 кг) (9,81 м / с 2 ) + (1000 кг) (9,81 м / с 2 ) = 1 + 2
=>
R 1 + R 2 = 14715 N
= 14.7 кН
Алгебраическая сумма моментов (2) может быть выражена как
(500 кг) (9,81 м / с 2 ) (1 м) + (1000 кг) (9,81 м / с 2 ) (6 м) =? R 1 (0 м) + R 2 (10 м)
=>
R 2 = 6377 (N)
= 6,4 кН
F 3 можно рассчитать как:
R 1 = (14715 Н) — (6377 Н)
= 8338 N
= 8338 N
. 2)`
Калькулятор момента пучка и поперечной силы
Мы используем эти уравнения вместе с граничными условиями и нагрузками для наших балок, чтобы получить замкнутую форму
решения для конфигураций балок, показанных на этой странице (балки с простой опорой и консольные балки).В
Калькулятор балок использует эти уравнения для расчета изгибающего момента, поперечной силы, наклона и прогиба.
диаграммы.Калькулятор балок — отличный инструмент для быстрой проверки сил в балках. Используйте это, чтобы помочь вам в дизайне
сталь, дерево
и бетонные балки при различных условиях нагружения. Также помните, что вы можете добавлять результаты из балок
все вместе
с использованием
метод
суперпозиция.Калькулятор стальных, деревянных и бетонных балок
Конечно, не всегда возможно (или практично) получить решение в замкнутой форме для некоторой балки.
конфигурации. Если у вас стальная, деревянная или бетонная балка со сложными граничными условиями и нагрузками
вам лучше решить проблему численно с помощью одного из наших инструментов анализа методом конечных элементов. Если
ты не
беспокоясь о конструктивных кодах и сравнивая потребность в луче и его пропускную способность, попробуйте наши простые в использовании
Калькулятор сдвига и момента.Если вам нужны полные проверки конструкции с помощью AISC 360, NDS, ASD и LRFD для конструкции стальных или деревянных балок
и вы хотите создать свой следующий луч за считанные минуты, вам может понравиться наш
Инструмент Beam Designer.Конструкция балок из стали по стандарту AISC и дерева NDS
Наша цель с WebStructural — вернуть инженерное сообщество, предоставляя бесплатные,
облачное приложение для проектирования стальных и деревянных балок.
Бесплатный Калькулятор Луча | Изгибающий момент, Калькулятор поперечной силы и прогиба
Добро пожаловать в наш бесплатный онлайн калькулятор изгибающего момента и диаграммы силы сдвига, который может генерировать реакции, Диаграммы силы сдвига (SFD) и диаграммы изгибающих моментов (BMD) консольной балки или опертой балки. Используйте этот калькулятор балок, чтобы определить реакции на опорах, нарисуйте диаграмму сдвига и момента для балки и рассчитайте прогиб стали или дерево луч. Бесплатный онлайн лучевой калькулятор для генерации реакций, расчет прогиба стальной или деревянной балки, составление диаграмм сдвига и момента для балки. Это бесплатная версия нашей полной SkyCiv. Beam Software. Доступ к нему можно получить в любом из наших Платные аккаунты, который также включает программное обеспечение для полного структурного анализа.
Используйте интерактивную рамку выше для просмотра и удаления длины луча, поддерживает и добавляет нагрузки. Любые сделанные изменения автоматически перерисовывают диаграмму свободного тела любым простым или консольным лучом.. Калькулятор реакции луча и расчеты изгибающего момента будут запущены, как только «Решить» нажата кнопка и автоматически сгенерирует диаграммы моментов сдвига и изгиба. Вы также можете нажать отдельные элементы этого калькулятора луча LVL, чтобы редактировать модель.
Калькулятор пролета луча легко рассчитает реакции на опорах. Умеет рассчитывать реакции на опорах для консольных или простых балок.. Это включает в себя расчет реакций для балки кантилевера, который имеет реакцию изгибающего момента, а также х,у сил реакции.
Вышеуказанный калькулятор балок со стальной балкой — это универсальный инструмент для расчета конструкций, используемый для расчета изгибающего момента в алюминии., деревянная или стальная балка. Его также можно использовать в качестве калькулятора грузоподъемности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Может вместить до 2 различные сосредоточенные точечные нагрузки, 2 распределенные нагрузки и 2 моменты. Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками. (UDL), треугольные распределенные нагрузки или трапециевидные распределенные нагрузки. Все нагрузки и моменты могут иметь как восходящее, так и нисходящее направление по величине., которые должны быть в состоянии учитывать наиболее распространенные ситуации анализа пучка. Расчет изгибающего момента и силы сдвига может занять до 10 секунд, чтобы появиться и, пожалуйста, обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, Диаграмма силы сдвига и диаграмма изгибающего момента балки.
Одна из самых мощных функций использует его в качестве калькулятора отклонения луча (или калькулятор смещения луча). Это может быть использовано для наблюдения расчетного отклонения балки с простой опорой или балки кантилевера. Возможность добавлять формы и материалы раздела, это делает его полезным в качестве калькулятора для деревянных балок или в качестве калькулятора для стальных балок для LVL-лучей или I-лучевой конструкции. На данный момент, эта функциональность доступна в SkyCiv Beam который имеет гораздо больше функциональных возможностей для древесины, конструкция из бетона и стальных балок.
SkyCiv предлагает широкий спектр программного обеспечения для анализа и проектирования облачных вычислений для инженеров. Как постоянно развивающаяся технологическая компания, мы стремимся к инновациям и стимулированию существующих рабочих процессов, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Балка (расчет) – Эксперт-Строй Про
В строительной инженерии несущая конструкция, рассчитанная на изгиб, называется «балка». Расчет этой конструкции – сложная, ответственная задача, от правильности зависит надежность и безопасность строительного объекта.
Расчет балки
Опорный элемент конструкции, на который возлагается некая нагрузка, применяется для строительства перекрытий и оформления дверных/оконных проемов. Оказываемые нагрузки имеют различный характер, определяемый видом конструкции.
Расчёт нагрузки на балку зависит от необходимой длины, нагрузки, шага укладки, если необходим расчет балок перекрытия. Процедура подразумевает построение эпюр, проведение сложных математических вычислений, но сегодня в интернете можно найти далеко не один онлайн-калькулятор, позволяющий провести экспресс расчёт консольной балки, расчет балки на прочность, жесткость, прогиб, прочее. Этот метод нельзя назвать точным, к нему лучше не прибегать, если хотите получить точный результат и надежную конструкцию.
Чтобы рассчитать нагрузку на балку, необходимо:
- составить рассечённую схему объекта;
- вычислить габариты, сечение, характеристики конструкции;
- определить характер нагрузки, найти точку ее приложения;
- рассчитать максимальную нагрузку на балку в этой точке.
К характеристикам относятся момент инерции и момент сопротивления, на основе которых происходит определение прочности и жесткости. Также важен такой показатель, как реакция опоры.
Разновидность перекрытий
Деревянный вид перекрытий для строительства частных домов, загородных коттеджей применятся наиболее часто. Железобетонные — чаще применяются для строительства многоэтажных зданий, металлические отличаются наименьшей применяемостью.
Чтобы провести расчет деревянных балок перекрытия, нужно выполнить замер пролета, определить способ и степень закрепления, вычислить постоянную и временную нагрузки. После этого программа-калькулятор, используя полученные данные, поможет выбрать шаг и сечение балок.
Расчет железобетонной балки более сложный, так как нужно учесть прочность бетона на нагрузку сжатием и арматуры на растяжение. Конструкция из ж/б выдерживает большие нагрузки, нежели деревянная.
Расчет металлической балки, как и расчет стальной балки, имеет свои особенности и проводится согласно СНиП II-23-81, где описаны требования и методический принцип вычислений.
Расчет при проведении строительной экспертизы
Обычно проводится расчет существующей конструкции с целью определения ее соответствия требованиям и оценки состояния. Но при перепланировке помещений и зданий, проведении реконструкционных работ (надстройка, пристройка, организация проемов) проводится расчет балки на прогиб, расчет балки на изгиб и прочие воздействия с целью обеспечения надежности.
Компания «Эксперт-Строй Про» предоставляет свои услуги в Москве и в Московской области. К нам можно обратиться, если понадобится расчет деревянной балки (стальной, железобетонной), а также при необходимости проведения экспертной оценки ремонтных / монтажных работ, для проведения технадзора за строительством, выполнения строительного аудита.
Полный перечень услуг можно найти на сайте, там же, в меню «Контакты» есть форма обратной связи, где можно задать интересующий вопрос. Также звоните нам по номеру +7 499 130 06 65 или пишите на электронный адрес [email protected].
Расчет прогиба балки методом начальных параметров
В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки, работающей на изгиб. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.
Теория по методу начальных параметров
Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым, охватим всю теоретическую часть по максимуму. Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:
Выбор базы и обозначение системы координат
Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Базу обозначим буквой O и проведем через нее систему координат:
Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях, упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом решения задач на метод начальных параметров.
Универсальное уравнение прогибов для балки
После введения базы, системы координат и обозначении расстояний а, б, в, г записываем универсальную формулу, с помощью которой, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки): Теперь поговорим об этой формуле, проанализируем так сказать:
- E – модуль упругости;
- I – момент инерции;
- Vk – прогиб сечения K;
- VO – прогиб сечения O;
- θO – угол поворота сечения О.
Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.
Итак, изучаем эту формулу с лева направо. В левой части уравнения обознается искомый прогиб, в нашем случае Vk, который дополнительно умножается на жесткость балки — EI:В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIVO:
Также всегда учитывается угол поворота сечения совпадающего с выбранной базой. Причем, произведение EIθO всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.
Следующие компоненты этого уравнения учитывают всю нагрузку находящуюся слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.
Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:
В случае с моментами, скоба возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен почасовой стрелке и отрицательным, соответственно, когда против часовой стрелки.
Учет распределенной нагрузки
Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки, но конец ее совпадает с сечением, прогиб которого мы хотим вычислить, поэтому в уравнение попадает только ее начало.
Причем важно, даже если бы в этом сечении была бы сила или момент, их бы так же не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.
Для распределенной нагрузки скобочка возводится в 4 степень и делится на 24. Правило знаков такое же, как и для сосредоточенных сил:
Граничные условия
Чтобы решить уравнение нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: VK, VO и θO. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и ни каких поворотов, то есть VO=0 и θO=0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.
Если бы балка была закреплена с помощью шарнирно подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был бы уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах.
Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров. Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.
Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:
Пример расчета прогиба балки
Для закрепления пройденного материала, предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок. Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·105 МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см4). Рассчитывать будем прогиб свободного торца, находящегося слева.
Подготовительный этап
Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки, проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:
В методе начальных параметров, есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае, рассматриваемый метод будет работать. В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м. от базы и заканчивается на 4 м. В таком случае, нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно-направленной нагрузкой. Тем самым, в расчете прогибов будет уже учитываться 2 распределенные нагрузки:
Расчет прогиба
Записываем граничные условия для заданной расчетной схемы:
VA = 0 при x = 6м
θA = 0 при x = 6м
Напомню, что нас, в этом примере, интересует прогиб сечения O (VO). Для его нахождения составим уравнение, для сечения A, в которое будет входить искомая величина:
В полученном уравнении, у нас содержится две неизвестные величины: искомый прогиб VO и угол поворота этого сечения — θO:
Таким образом, чтобы решить поставленную задачу, составим дополнительное уравнение, но только теперь, не прогибов, а углов поворотов, для сечения A:Из второго уравнения, найдем угол поворота:После чего, рассчитываем искомый прогиб:
Таким образом, свободный торец такой балки, прогнется практически на 6 см. Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае, для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.
Расчет стальной балки на прогиб
При расчете стальных балок по II-й ГПС (по прогибам) необходимо создавать раскрепления для прогибов:
Информация из справки LIRA SAPR (Справка\Пояснения Сталь\Проверки прогибов):
Проверка прогиба осуществляется сопоставлением реально определенного относительного прогиба (L/f) с максимально возможным для данного конструктивного элемента прогибом.
В данной версии проверка выполняется только для балок на основании состава загружений во всех сочетаниях. Учитываются коэффициенты надежности по нагрузке (заданные при формировании РСУ в среде ПК ЛИРА-САПР) и коэффициенты сочетания.
Перемещения, вызванные загружениями с долей длительности 0, в данном расчете не используются.
Прогибы находятся для каждого сечения на основании распределения MY1, MZ1, QY1, QZ1 по длине элемента. Соответственно, увеличение количества расчетных сечений способствует более точному определению прогибов (особенно, если воздействуют сосредоточенные силовые факторы).
В режиме локального расчета элемента (см. справочную систему СТК-САПР) имеется возможность расчета прогибов по огибающим эпюрам изгибающего момента в запас. Это может потребоваться, когда редактируются расчетные сочетания усилий (или нагрузок) и теряется связь с результатами расчета на ПК ЛИРА-САПР основной схемы.
Важно: Предусмотрена возможность определять не чистые перемещения (относительно локальных осей Y и Z в недеформированной схеме), а прогиб относительно двух выбранных условно неподвижных точек – точек раскрепления (в случае консоли, например, относительно одной точки).
Схема к определению прогибов балки с раскреплениями и без раскреплений
На приведенном фрагменте показан механизм определения прогибов (они обозначены как di и dk) в конструктивном элементе с наложенными раскреплениями на элементы.
Если раскрепления не наложены, то прогиб принимается равным полному расстоянию до оси X.
Важно: Если балка (ригель) разбита по длине промежуточными узлами, то для нее необходимо создать конструктивный элемент и раскрепления для проверки прогибов создавать как для конструктивного элемента (т.е. для балки как единого целого). В расчете стальных конструкций коэффициент расчетной длины (и для балок, и для колонн, и для ферм) применяется к длине конечного элемента (КЭ), если не задан конструктивный элемент (КоЭ). Если задан КоЭ, то коэффициент расчетной длины применяется к полной длине КоЭ.
Пример расчета однопролетной балки
Расчётная модель рамы с цельным ригелем и разбитым на отдельные элементы
Согласно нормативной документации прогиб определяется от действия нормативных нагрузок. Поскольку в LIRA SAPR все нагрузки прикладываются к узлам и элементам их расчётными значениями, при определении прогибов программа определяет нормативное значение нагрузок путём деления их на коэффициент надёжности.
Посмотреть какие приняты коэффициенты надёжности, а также ввести их вручную, если это необходимо, можно в окне параметров расчёта.
Окно параметров расчёта, вызываемое из окна задания параметров для стальных конструкций
Подробнее о корректировке коэффициентов надёжности для расчета прогибов вручную читайте в статье «Коэффициенты к временным нагрузкам при проверке прогиба»
Мозаика результатов проверки назначенных сечений по 2 предельному состоянию
Предельно допустимый L/200=6000/200=30мм
Без задания раскреплений (по абсолютному перемещению узлов балки):
((39,8мм/ к-т надежности по нагрузке)/ 30мм))*100%=((39,8/1,1)/30)*100%=120,6%
С заданием раскреплений (по относительному перемещению узлов балки за вычетом перемещений опорных узлов):
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%
Ручной ввод расчётной длины балки для расчёта прогибов
В диалоговом окне задания характеристик расчёта стальной балки присутствует группа параметров Расчёт по прогибу.
Информация из справки ЛИРА САПР:
Расчет по прогибу – данные для расчета прогиба. Длина пролета авто – вычисляется по положению раскреплений. Длина пролета точно – длина пролета при расчете приравнивается этому числу.
Рассмотрим раму из предыдущего примера, только теперь раскрепления для прогибов назначим для всех конструкций, а расчётные длины будем для первого случая задавать автоматическим способом, а для второго ручным.
Расчётная модель с информацией о назначенных расчётных длинах балок
Результаты расчётов прогибов балок
Предельно допустимый прогиб при длине 6 м L/200=6000/200=30мм
Предельно допустимый прогиб при длине 4 м L/200=4000/200=20мм
Проценты использования по предельному прогибу
Длина балки 6 м:
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%
Длина балки 4 м:
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/20)*100%=139,4%
Расчёт прогибов стрельчатой арки
Пример — рама переменного сечения (РПС) пролётом 18 м. Соединение полурам в коньке — шарнирное, опирание полурам на фундамент — шарнирное.
Расчётная модель рамы
При этом в параметрах «Дополнительные характеристики» необходимо указать вручную пролет, с которым программа будет сравнивать прогиб (автоматическое определение пролета возможно только для линейных балок, где все конечные элементы (КЭ) конструктивного элемента (КоЭ) лежат на одной оси):
Эпюра перемещений fz ригеля одной полурамы (вдоль местной оси Z1 стержня)
Мозаика перемещений узлов по Z и «Раскрепления для прогибов» (раскреплён только ригель №4)
Результаты определения прогибов в СТК-САПР:
Результаты определения прогибов ригелей №2 и №4
Предельно допустимый L/200=17664/200=88.32 мм
Без задания раскреплений (по абсолютному значению на эпюре прогибов fz):
96.7/17644=1/182 — совпадает с результатом расчёта элемента №2
С заданием раскреплений (по относительному значению на эпюре прогибов fz):
(96.7-(-6.46))/17644=1/171 — совпадает с результатом расчёта элемента №4
Без задания раскреплений (по абсолютному значению перемещений узлов):
99.8/17644=1/177 — не совпадает ни с чем
Вывод: Расчёт на прогибы выполняется в местной системе координат стержня. Прогиб стрельчатых и цилиндрических арок, а также любых криволинейных конструкций, нужно определять по перемещениям узлов в глобальной системе координат и вручную сравнивать с предельно допустимыми значениями.
Расчёт прогибов цилиндрической арки
Пример – цилиндрическая арка пролётом 18 м, стрелой подъёма f = 9 м. Соединение всех элементов между собой — жёсткое, опирание на фундамент — шарнирное.
Нагрузки на арку приложены их расчётными значениями. Значения нагрузок для определения прогибов принимаются согласно СП 20.13330.2016 Нагрузки и воздействия, таблица Д.1 Приложения Д. В данном примере арка является конструкцией покрытия, прогиб которой должен определяться от постоянных и длительных нагрузок (п.2 табл. Д.1). Для визуализации перемещений от нормативных значений нагрузок, необходимо создать особое РСН с нормативными длительными значениями нагрузок. Нагрузки в данном РСН нужно поделить на коэффициент надёжности, с учётом длительности. На конструкцию действуют два загружения:
Загружение 1 — постоянное, коэффициент надёжности 1.1;
Загружение 2 — кратковременное, коэффициент надёжности 1.2, доля длительности 0.35;
Вычислим коэффициенты для перехода к нормативным значениям
Загружение 1 Kn=1/1.1=0.91;
Загружение 2 Kn=1/1.2*0.35=0.292
Таблица РСН с сочетаниями расчётных и нормативных значений нагрузок с учётом длительности.
Мозаика перемещений узлов цилиндрической арки от РСН2
Предельно допустимый прогиб L/200=18000/200=90 мм
Фактический прогиб (по абсолютному значению перемещений узлов): 32.2/18000=1/559 – меньше предельно допустимого значения.
Примечание: если подобная конструкция стоит на своих опорах, то перемещения опорных точек (для получения относительных перемещений) удобно получить через «Мозаику относительных перемещений», указав реперный узел.
Мозаика перемещений узлов в глобальной СК (абсолютных)
Мозаика перемещений узлов в глобальной СК относительно реперного узла
Прокатная балка онлайн
Момент сопротивления слишком большой, возможны большие перенапряжения! Перенапряжение должны быть не более 5%! Скорее всего нужного профиля в сортаменте (ГОСТ 8239-72) нет, попробуйте найти ГОСТ 26020-83.
Значение опорных реакций (положительная — направлена вниз, отрицательная — вверх):
RA=
кН
RB=
кН
Значение усилий в произвольном сечении:
Координата x=
2345678910СправаСлева
Значение эпюры Q при x=
м:
кН
Значение эпюры M при x=
м:
кН·м
Значение эпюры
при x=
м:
кН·м²·рад
Значение эпюры
при x=
м:
кН·м³
Начальные параметры:
кН
кН·м
кН·м²·рад
кН·м³
Максимальные значения усилий:
Подбор поперечного сечения.
Нужный момент сопротивления:
тр см 3
Из таблицы сортамента (ГОСТ 8239-72) принимаем двутавр №, с такими геометрическими характеристиками:
см4;
см3;
см3.
Размеры сечения:
мм;
мм;
мм;
мм.
Полная проверка прочности балки.
а) По максимальным нормальным напряжением (сечение
при
м).
МПа
% — недонапряжение.
перенапряжение.
б) По максимальным касательным напряжением (сечение
при
м).
МПа
% — недонапряжение.
перенапряжение.
Вычисляем статический момент полки двутавра относительно центральной оси
:
см3,
касательное напряжение в точке стыка полки и стенки:
МПа.
в) Главные напряжения проверяем в (сечение
при
м,
СправаСлева).
Усилия в сечении:
кН·м,
кН.
Определяем нормальное и касательное напряжение в точке стыка полки и стенки двутавра:
МПа;
МПа.
По четвертой теории прочности:
МПа
% — недонапряжение.
перенапряжение.
Определяем касательное напряжение на нейтральной оси:
МПа.
Эпюра поперечных сил:
Определить максимум на эп. Q
Эпюра изгибающих моментов:
Определить максимум на эп. M
Эпюра углов поворота:
Определить максимум на эп. EIφ
Эпюра прогибов:
Определить максимум на эп. EIw
Калькулятор
для инженеров — изгибающий момент и поперечное усилие для балки с простой опорой
Избранные ссылки
Калькулятор преобразования напряжения
Расчет главного напряжения, максимального напряжения сдвига и их плоскостей
Калькулятор для анализа подвижной нагрузки
Для определения абсолютного макс. Б.М. из-за движущихся грузов.
Калькулятор преобразования напряжения
Расчет главного напряжения, максимального напряжения сдвига и их плоскостей
Калькулятор момента инерции
Расчет момента инерции плоских секций e.грамм. швеллер, уголок, тройник и др.
Калькулятор железобетона
Расчет прочности железобетонной балки
Калькулятор распределения моментов
Решение неопределенных балок
Калькулятор прогиба и уклона
Расчет прогиба и уклона свободно опертой балки для многих случаев нагружения
Калькулятор фиксированной балки
Инструмент для расчета изгибающего момента и поперечной силы для фиксированной балки для многих случаев нагружения
Калькулятор BM и SF для консоли
Расчет SF и BM для консоли
Калькулятор прогиба и наклона консоли
Для многих случаев нагружения консоли
Вычислитель выступающей балки
Для SF и BM многих случаев нагружения выступающей балки
Дополнительные ссылки
Викторина по гражданскому строительству
Проверьте свои знания по различным темам гражданского строительства
Научные статьи
Научные статьи, диссертации и диссертации
Небоскребы мира
Высокие здания во всем мире
Предстоящие конференции
Список конференций, семинаров и практикумов по гражданскому строительству
Профиль инженеров-строителей
Познакомьтесь с выдающимися инженерами-строителями
Профессиональные общества
Всемирные профессиональные общества инженеров-строителей
Продолжайте посещать, чтобы получать обновления, или присоединяйтесь к нашему списку рассылки, чтобы получать обновления
Поищите на нашем сайте больше…
Расскажите о нас друзьям
Другие полезные ссылки
Онлайн калькулятор луча
| Калькулятор изгибающего момента и силы сдвига выступающей балки
NEWS | ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ | ЛИСТ
Бесплатный онлайн-калькулятор предназначен для расчета величины поперечной силы и изгибающего момента в точке свисающей балки, несущей равномерно распределенную нагрузку (UDL), или точечной нагрузки в любой точке по длине.
Он даже обеспечивает количество наивысшего изгибающего момента, в котором его местоположение появляется. Калькуляторы соответствуют установленным формулам для поперечной силы и изгибающего момента нависающей балки и предложены преподавателями колледжа.
В случае объединения нагрузок можно реализовать закон суперпозиции для вычисления результирующих величин.
Примеры нагрузки для выступающей балки: калькулятор предлагает результаты для поперечной силы и изгибающего момента на части выступающей балки, вероятно, по отношению к точечной нагрузке на пролете.Вычисленные величины можно использовать для набросков изгибающего момента и поперечной силы.
Калькулятор также можно использовать для определения ординат диаграммы линий влияния для зданий.
Равномерная нагрузка на балку: калькулятор предлагает результаты для поперечной силы и изгибающего момента на части выступающей балки, вероятно, в отношении равномерно распределенной нагрузки на участке пролета. Пожалуйста, сделайте ссылку на представление и введите количество нагрузки и пролеты в форму, представленную ниже, а затем нажмите «Рассчитать».
Предполагается, что все восходящие рабочие нагрузки положительны, а нисходящие — отрицательны.
Онлайн-калькуляторы изгибающего момента и поперечной силы выступающей балки.
Пройдите следующий видеоурок, чтобы получить дополнительную информацию.
Лектор: Параг Пал
Диаграммы внутренних сил для двухопорной балки
Этот онлайн-калькулятор показывает диаграммы внутренних сил для простой (двухопорной) балки, закрепленной на одном конце и поддерживаемой роликом на другом, под системой нагружения.Калькулятор графически отображает изгибающий момент M и поперечную силу Q, действующие вдоль стержня. Чертеж необходим для определения положения наиболее нагруженного (опасного) участка балки.
Теория и формулы расчета находятся под калькулятором.
Просто введите данные системы нагружения в приведенную ниже таблицу и получите диаграммы свободного тела, усилия сдвига и изгибающего момента.
Сила сдвига и изгибающий момент в двухопорной балке
Нагрузка
шт. На странице:
Нагрузка
Может быть отрицательной, если нагрузка слева от опоры A
Нагрузка Сила, кН Равномерно распределенная нагрузка, кН / мл Линейно распределенная нагрузка, кН / м Момент, кН * м Направление момента По часовой стрелке Против часовой стрелки Разница Уменьшить Увеличить Сохранить Сохранить
Отмена
Импорт данных Ошибка импорта
«Для разделения полей данных используется один из следующих символов: табуляция, точка с запятой (;) или запятая (,)» Пример: -50.5; L; 50,5; вверх; против часовой стрелки; 50,5; увеличить
Загрузить данные из файла .csv.
Импорт
Назад
Отмена
Точность расчета
Цифры после десятичной точки: 2
Диаграммы поперечного усилия и изгибающего момента
Файл очень большой. Во время загрузки и создания может произойти замедление работы браузера.
Скачать
Файл очень большой. Во время загрузки и создания может произойти замедление работы браузера.
Скачать
Ссылка Сохранить Виджет
Внутренние силы
На следующем рисунке показаны внутренние силы в балке под нагрузкой.
Балка под нагрузкой. Внутренние силы в разрезе.
Чтобы определить внутренние силы в точке B, проведем воображаемый участок, перпендикулярный оси x, вдоль осей y и z.
Схема свободного тела сегментов балки
Схема свободного тела сечения балки показывает внутренние силы, действующие в точке B, как внешние. Составляющая силы N B , действующая вдоль оси x, называется нормальной силой . Мы пропускаем расчет нормальной составляющей силы в калькуляторе, поскольку он допускает только нагрузки, действующие перпендикулярно балке.
Составляющая внутренней силы Q B , действующая параллельно поперечному сечению, называется поперечной силой . Калькулятор получает только y-компонент силы шептала, поскольку z-компонент равен нулю для перпендикулярных нагрузок.
Момент пары M B называется изгибающим моментом .
Изгибающий момент равен сумме всех силовых моментов, приложенных к сегменту балки относительно центра тяжести сечения.
Составляющие силы предотвращают относительное перемещение между двумя сегментами, а момент пары предотвращает относительное вращение.
Диаграммы внутренних сил путем интегрирования.
Мы найдем формулы для расчета значений поперечной силы Q (x) и изгибающего момента M (x) отдельно для разных участков балки.
На границах сегментов есть выступающие точки: концы балок, места опор, точки приложения сосредоточенных сил и сосредоточенных моментов, границы распределенных нагрузок.
Для каждого сегмента вычисляется интеграл функции распределенной нагрузки q (x) для определения поперечной силы Q (x).Следующим шагом является вычисление интеграла от Q (x) для определения функции изгибающего момента M (x) в соответствии с формулами:
Распределенная нагрузка q (x) в нашем калькуляторе может быть линейной, линейно убывающей или возрастающей. В первом случае q (x) — константа, во втором — линейная функция: q (x) = kx + b. При отсутствии распределенных нагрузок в сечении поперечная сила будет постоянной.
Таким образом, чтобы найти функции Q (x), а также M (x), необходимо будет получить неопределенный интеграл от полинома и вычислить постоянную интегрирования.Константу интегрирования можно легко найти, если мы знаем некоторую точку, через которую проходит требуемая функция. См .: Полиномиальный интеграл.
В качестве такой точки мы возьмем значения Q (x) и M (x) вдоль левой границы каждого сегмента.
Q (x l ) будет равно значению функции поперечной силы для предыдущего сегмента в самой правой точке сегмента плюс величина сосредоточенной силы (или реакции опоры) в этой точке, если таковая имеется. Если сила действует вверх, то изменение Q (x) будет положительным или отрицательным в противном случае.
M (x l ) будет равно значению функции изгибающего момента M (x) для предыдущего сегмента в его крайней правой точке, сдвинутому на значение сосредоточенного момента, приложенного к этой точке, если таковой имеется. Если сосредоточенный момент направлен по часовой стрелке, то сдвиг положительный, в противном случае — отрицательный.
Значение Q (x) на левом крае балки будет соответствовать сумме сосредоточенных сил и реакции опоры в этой точке или будет равно нулю, если их нет.Значение M (x) на концах балки равно сумме значений сосредоточенных моментов, приложенных к концам балки. Если в этих точках нет сосредоточенных моментов, то M (x) будет равно нулю.
Знаки M (x) и Q (x) могут быть связаны с характером деформации балки под действием внешних сил. Если изгибающий момент в сечении положительный, то балка в этом сечении прогибается выпуклостью вниз, если отрицательная, то балка сгибается выпуклостью вверх.
Пример
Рассмотрим расчет Q (x) и M (x) на примере:
Схема свободного тела с двумя опорными балками
Откройте этот пример в калькуляторе.
- Во-первых, найти реакцию поддержки. Вы можете увидеть, как это сделать, на этой странице.
Расчетные опорные реакции: - Разделить луч на сегменты по ключевым точкам: 0, 2, 4, 5, 6.
Отрезок А — граничные точки: 0,2
Отрезок В — граничные точки: 2,4
Участок С — граничные точки: 4,5
Участок D — граничные точки: 5,6 - Для каждого сегмента:
Сегмент B, граничные значения
Сегмент B
Чтобы найти функцию распределенной нагрузки q (x), мы используем линейное уравнение из двух точек.
По точкам (2; 0) и (4; 8) мы можем найти это уравнение: q (x) = 4x-8.
Интегрируйте эту функцию, чтобы найти формулу силы сдвига.
По формуле Q (x) предыдущего отрезка вычислите Q на левой границе: Q (2) = — 5 ∙ 2 + 11,56 = 1,56. Аналогично предыдущему сегменту найдите интеграл и постоянную интегрирования по точке (2; 1.56).
Формула силы сдвига сегмента B:
см. Расчет
Найдите значение момента в точке x = 2 по формуле предыдущего сегмента M (x): M (2) = -2.5 ∙ 2 2 + 11,56 ∙ 2 + 0 = 13,12.
Интегрируя Q (x) и вычисляя постоянную интегрирования по левому граничному значению , получаем формулу изгибающего момента для сегмента B:
см. Расчет
Сегмент C, граничные значения
Сегмент C
Рассчитайте поперечную силу в точке 4 по формуле поперечной силы Q (x) сегмента B: Q (4) = -2 ∙ 4 2 + 8 ∙ 4 — 6,44 = -6,44.
Сосредоточенная сила F 1 = 4 кН резко изменяет значение Q (x) в точке x = 4.Он направлен вниз, поэтому сложение отрицательное: Q (4) = -6,44 — 4 = -10,44
На этом сегменте нет распределенной нагрузки, поэтому поперечная сила постоянна.
Формула силы сдвига сегмента C:
Значение изгибающего момента в точке x = 4 рассчитывается по формуле M (x) для предыдущего сегмента: M (4) = -0,67 ∙ 4 3 + 4 ∙ 4 2 — 6,44 ∙ 4 + 15,33 = 10,91
Проинтегрируйте Q (x) и вычислите C по граничному значению получите формулу изгибающего момента сегмента С:
см. Расчет
Сегмент D, граничные значения
Сегмент D
Поскольку распределенная нагрузка отсутствует, поперечная сила на этом участке постоянна.
Сила сдвига сегмента D:
Рассчитайте граничное значение M (5) по предыдущей формуле M (x): M (5) = -10,44 ∙ 5 + 52,67 = 0,47
Сосредоточенный момент M 1 изменяется M x на данный момент. Сосредоточенный момент направлен по часовой стрелке, поэтому добавление положительное: M (5) = 0,47 + 10 = 10,47
Интегрируем Q (x) и получаем C , получаем формулу изгибающего момента для сегмента D:
см. Расчет
Найдите крайние правые Q (x) и M (x), чтобы убедиться, что мы нашли правильную формулу:
Абсолютное значение поперечной силы равно значению реакции опоры в этой точке.Как и ожидалось, изгибающий момент на конце балки равен нулю.
Калькулятор стальной балки
— подробные расчеты за считанные минуты
Для каких проектов подходят калькуляторы?
Калькуляторы предназначены для бытовых проектов.
Мне нужен только единичный расчет, мне он подходит?
Да, просто оформите ежемесячную подписку и отмените ее, как только закончите.
Учитываются ли в калькуляторах стали европейские размеры сечения?
Да, калькулятор стальной балки Еврокода включает профили IPE и другие стандартные европейские размеры сечений.Он также включает разделы UB, UC и PFC. Объекты британской секции предоставлены Tata Blue Book, европейские секции предоставлены ArcellorMittal Orange Book.
Могу ли я использовать стандартные / метрические единицы измерения США?
Во всех калькуляторах используются метрические единицы, кроме калькулятора США, в котором используются стандартные единицы измерения США.
В каком формате бывают отчеты?
Расчеты можно загрузить или отправить по электронной почте в виде файла PDF.
Что мне делать, если мне нужна нагрузка, которой нет в раскрывающемся списке?
Если вам нужно использовать нагрузку, которой нет в раскрывающемся меню, выберите «другое» внизу списка и введите сведения о нагрузке вручную.
Будут ли калькуляторы работать на моем ПК / Mac / планшете?
Да, калькуляторы работают в вашем браузере на любом устройстве, подключенном к Интернету, включая ПК, Mac и планшеты.
Насколько точны калькуляторы?
Мы сравниваем калькуляторы с различными источниками. К ним относятся примеры организаций по стандартизации, институтов, торговых организаций и учебники. Мы также сравниваем наши результаты с другими инженерными программами.
Мы используем автоматизированные модульные тесты и сквозные тесты для моделирования десятков или сотен примеров расчетов, охватывающих широкий спектр сценариев использования для каждого калькулятора.
Мы также используем наши основные вычислительные машины для воссоздания и сравнения наших результатов со стандартными отраслевыми таблицами (такими как Синяя книга, Оранжевая книга и таблицы пролетов древесины).
Наши калькуляторы обычно проходят недели или месяцы бета-тестирования и итераций и, наконец, перед выпуском на рынок независимым дипломированным инженером-строителем.
Заявление об ограничении ответственности: Все программное обеспечение для проектирования основано на приблизительных оценках и стандартах, которые могут быть открыты для интерпретации и могут изменяться.Вы должны использовать эти калькуляторы только в том случае, если у вас достаточно знаний, чтобы правильно оценить нагрузки, поддерживаемые элементами, обоснованность вывода программы, общую производительность конструкции и пригодность предлагаемой конструкции. Результаты следует проверять на себе, а все расчеты проверять самостоятельно.
Калькулятор и таблица веса двутавровой балки и двутавровой балки (бесплатно)
Что такое я балка
Балка двутавровая Сталь
Двутавровая балка также называется стальной балкой (Universal Beam), которая представляет собой длинную стальную полосу с поперечным сечением двутавровой формы.Двутавровая балка делится на обыкновенную двутавровую и световую двутавровую.
Что такое двутавровая балка
Двутавровая балка разработана на основе оптимизации двутавровой стали. Название получено из-за того, что его сечение совпадает с английской буквой H. Это экономичный высокоэффективный профиль с более разумным соотношением прочности к весу и более оптимизированным распределением площади поперечного сечения.
Каждая часть H-образной стали расположена под прямым углом, поэтому она обладает такими преимуществами, как сильное сопротивление изгибу, экономия затрат, простая конструкция и легкий вес во всех направлениях.
Часто используется в больших зданиях, где требуется большая перехватывающая способность и хорошая стабильность поперечного сечения, например, в высотных зданиях и мастерских. Кроме того, он также широко используется на судах, мостах, подъемно-транспортном оборудовании, кронштейнах, фундаментах оборудования, фундаментных сваях и т. Д.
Двутавровая балка и двутавровая балка
Что касается разницы между двутавровой балкой и двутавровой балкой, вы можете обратиться к статье ниже.
Двутавровая балка и двутавровая балка из стали (14 анализ различий)
Расчет веса двутавровой балки и расчет веса двутавровой балки
В этой статье мы в основном обсуждаем, как рассчитать вес двутавровой и двутавровой балок.
Для удобства расчета мы создали два калькулятора: калькулятор веса двутавровой балки и калькулятор веса двутавровой балки.
С помощью этих двух калькуляторов вы можете легко рассчитать вес двутавровой балки и двутавровой балки.
Конечно, для более подробных расчетов различных металлических весов вы можете обратиться к следующей статье.
Теоретическая формула расчета веса металла (30 типов металлов)
Кроме того, мы также сделали калькулятор тоннажа листогибочного пресса и калькулятор усилия прессования.Если вам интересно, вы можете воспользоваться им, перейдя по ссылке.
Теперь начните использовать калькулятор для расчета веса профиля.
Если вы устали использовать калькулятор для расчета веса двутавровой балки и двутавровой балки, вы можете обратиться к следующей таблице веса двутавровой балки и таблице веса двутавровой балки. Это позволяет быстрее проверять вес двутавровых и двутавровых балок разных размеров.
Поделиться — это забота!
Онлайн-структурное проектирование
Бесплатно
Расчет закрепленной балки (дюймовые)
Расчет бесплатный, логин не требуется
Расчет внутренних сил балки (поперечная сила, изгибающий момент) и прогибов
имперский
луч
приколот
грузы
случаи нагрузки
силы
отклонение
Открыть расчетный лист
Бесплатно
Луч, фиксированный на обоих концах (дюймовые)
Расчет бесплатный, логин не требуется
Расчет внутренних сил балки (поперечная сила, изгибающий момент) и прогибов
имперский
луч
фиксированный
грузы
случаи нагрузки
силы
отклонение
Открыть расчетный лист
Бесплатно
Расчет закрепленной балки (метрическая система)
Расчет бесплатный, логин не требуется
Расчет внутренних сил балки (поперечная сила, изгибающий момент) и прогибов
метрика
луч
грузы
случаи нагрузки
силы
отклонение
Открыть расчетный лист
Бесплатно
Балка, фиксированная на обоих концах (метрическая система)
Расчет бесплатный, логин не требуется
Расчет внутренних сил балки (поперечная сила, изгибающий момент) и прогибов
метрика
луч
фиксированный
грузы
случаи нагрузки
силы
отклонение
Открыть расчетный лист
Бесплатно
Емкость RC-балки (EC2)
Бесплатно, на ограниченный период, требуется логин
Расчет прочности на изгибающий момент железобетонной балки (Еврокод 2)
метрика
EC2
луч
конкретный
Открыть расчетный лист
Предварительный просмотр
Бесплатно
Прочность на изгиб стальной балки (дюймовая)
Бесплатно, на ограниченный период, требуется логин
Расчет прочности при изгибе стальной балки и поперечной устойчивости при кручении (AISC, LRFD)
имперский
луч
изгиб
сталь
LRFD
AISC
Открыть расчетный лист
Предварительный просмотр
Бесплатно
Стальной элемент жесткости подшипника балки (дюймовая)
Бесплатно, на ограниченный период
Проверьте требования к опорному элементу жесткости для стенок с сосредоточенными силами; Веб-локальная урожайность; Web Crippling; Боковое изгибание полотна
имперский
луч
сеть
уступающий
калечащий
коробление
LRFD
AISC
Открыть расчетный лист
Предварительный просмотр
Бесплатно
Диаметр балки (EC5)
Бесплатно, на ограниченный период, требуется логин
Расчет несущей способности деревянных балок, проверка деревянных элементов (Еврокод 5)
метрика
EC5
луч
древесина
изгиб
Открыть расчетный лист
Предварительный просмотр
Бесплатно
Емкость RC-балки (ACI318)
Бесплатно, на ограниченный период, требуется логин
Расчет прочности на изгибающий момент железобетонной балки (ACI 318)
имперский
ACI318
луч
изгиб
конкретный
Открыть расчетный лист
Предварительный просмотр
Бесплатно
Простая балка — равномерно распределенная нагрузка
Расчет бесплатный, логин не требуется
Расчет сдвигов, моментов и прогибов для простой опорной балки при равномерно распределенной нагрузке
метрика
статика
грузы
силы
луч
Открыть расчетный лист
Бесплатно
Простая балка — сосредоточенная нагрузка в центре
Расчет бесплатный, логин не требуется
Расчет сдвигов, моментов и прогибов для простой опорной балки с сосредоточенной нагрузкой в центре
метрика
статика
грузы
силы
луч
Открыть расчетный лист
Бесплатно
Простая балка — сосредоточенная нагрузка в любой точке
Расчет бесплатный, логин не требуется
Расчет сдвигов, моментов и прогибов для простой опорной балки, сосредоточенной нагрузки в любой точке
метрика
статика
грузы
силы
луч
Открыть расчетный лист
Бесплатно
Простая балка 2 Концентрированная сим.грузы
Расчет бесплатный, логин не требуется
Расчет сдвигов, моментов и прогибов для простой опорной балки, 2 сосредоточенных симметричных нагрузки
метрика
статика
грузы
силы
луч
Открыть расчетный лист
Бесплатно
Простая балка 2 Концентрированная сим.грузы
Расчет бесплатный, логин не требуется
Расчет сдвигов, моментов и прогибов для простой опорной балки, 2 сосредоточенных симметричных нагрузки
имперский
статика
грузы
силы
луч
Открыть расчетный лист
Бесплатно
Простая балка — равномерно распределенная нагрузка
Расчет бесплатный, логин не требуется
Расчет сдвигов, моментов и прогибов для простой опорной балки при равномерно распределенной нагрузке
имперский
статика
грузы
силы
луч
Открыть расчетный лист
Калькулятор изгибающего момента и поперечного усилия
Диаграмма момента изгиба.com — это бесплатный онлайн-калькулятор, который создает диаграммы изгибающего момента (BMD) и диаграммы поперечного усилия (SFD) для большинства простых балок. Калькулятор полностью настраивается для работы с большинством балок; эта функция недоступна в большинстве других калькуляторов. Программное обеспечение работает на базе SkyCiv, предлагая мощное программное обеспечение для структурного анализа и проектирования в облаке.
Инструмент полностью функциональный, поэтому посетите наше Бесплатное программное обеспечение Beam, чтобы начать работу! Он будет работать со всеми опорными, определяющими балками и способен воспринимать точечные нагрузки, сосредоточенные моменты и распределенные нагрузки.Кроме того, его можно легко настраивать и настраивать, чтобы вы могли создавать свои собственные лучи. Это чрезвычайно точный инструмент и, в отличие от современных калькуляторов, очень удобный. Это чрезвычайно полезный инструмент для студентов университетов, колледжей и старшеклассников, которым утомительно приходится перерисовывать BMD и SFD для заданий и практических / учебных вопросов.
У нас также есть учебная страница, которая поможет студентам университетов с расчетами, ожидаемыми в их инженерной степени, а также студентам старших классов.Эти студенты могут научиться рассчитывать и создавать диаграммы поперечной силы и изгибающего момента, и мы понимаем, что процесс анализа балки иногда может быть трудным, поэтому мы предоставили простое пошаговое руководство по расчету диаграмм изгибающего момента и поперечной силы. Включены простые уравнения и формулы изгибающего момента, которые хорошо помогают в ваших расчетах. Существуют также примеры и генераторы случайных балок, которые позволят вам поэкспериментировать с тем, как различные нагрузки влияют на расчет балки, а также на поперечную силу и изгибающий момент балки.
Схема
Bending Moment Diagram разработана командой SkyCiv Engineering, которая предлагает студенческие и профессиональные пакеты, которые предоставляют пользователям доступ к разнообразному программному обеспечению для проектирования конструкций для выполнения работы.

 071
071 18
18 503
503 71
71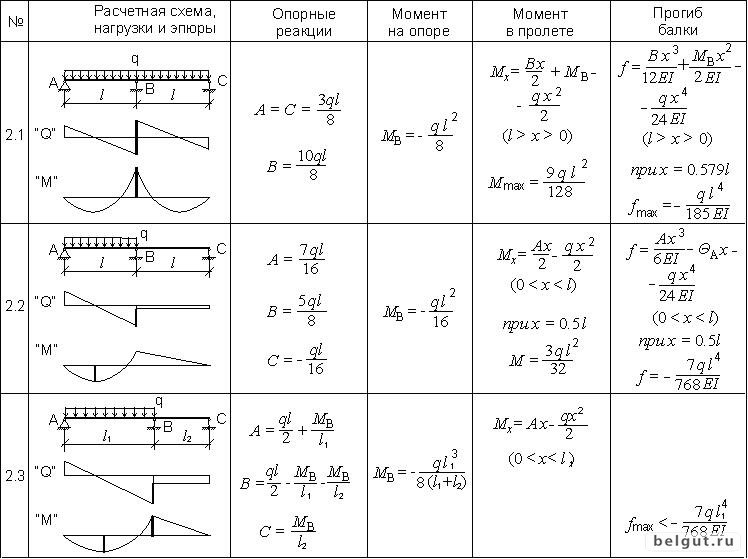 011
011 7
7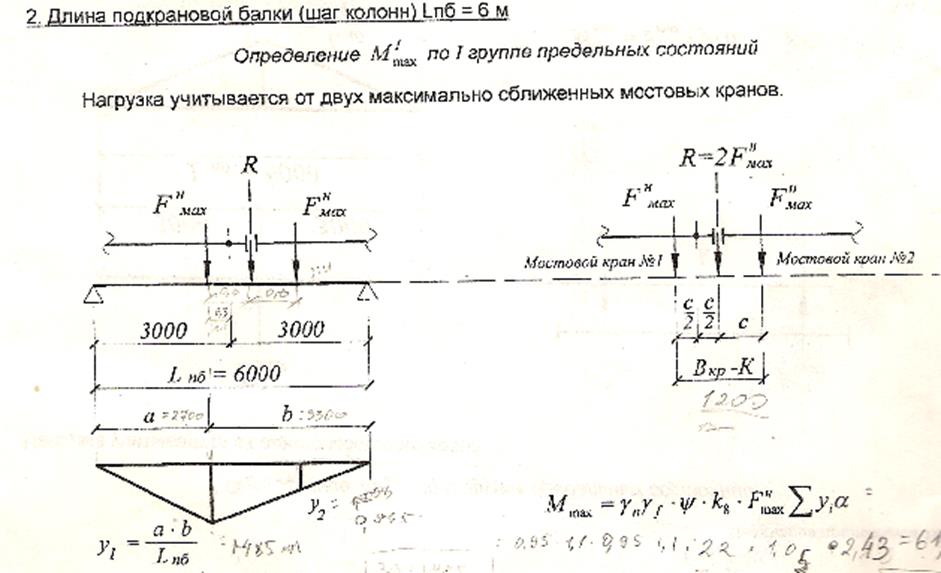 18
18 179
179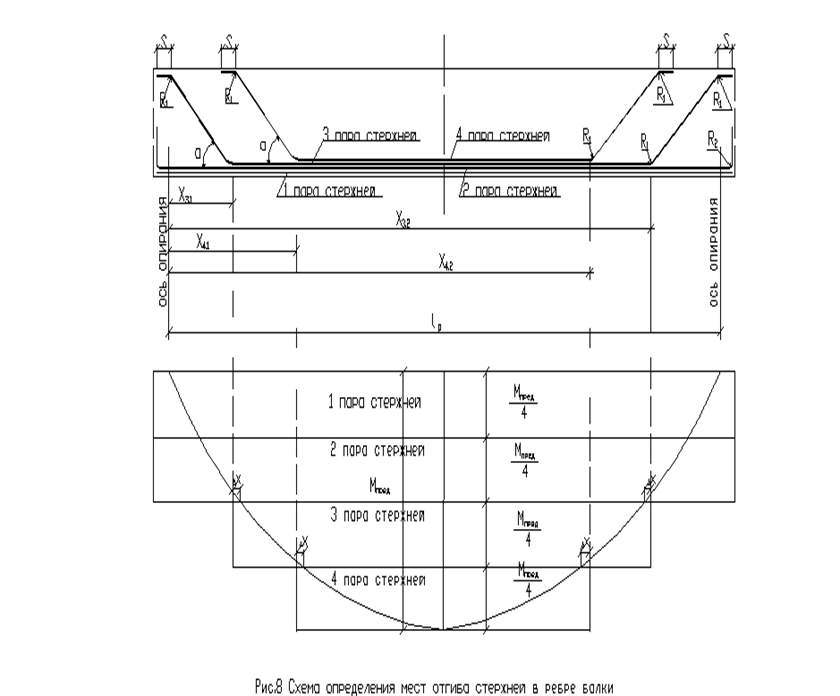 52
52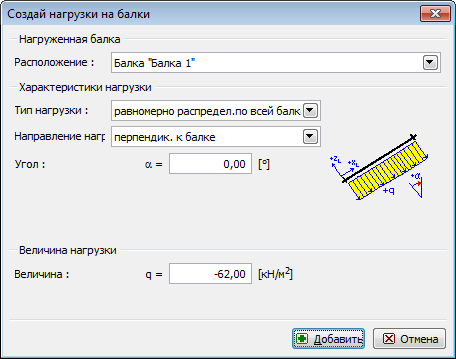 84
84 27
27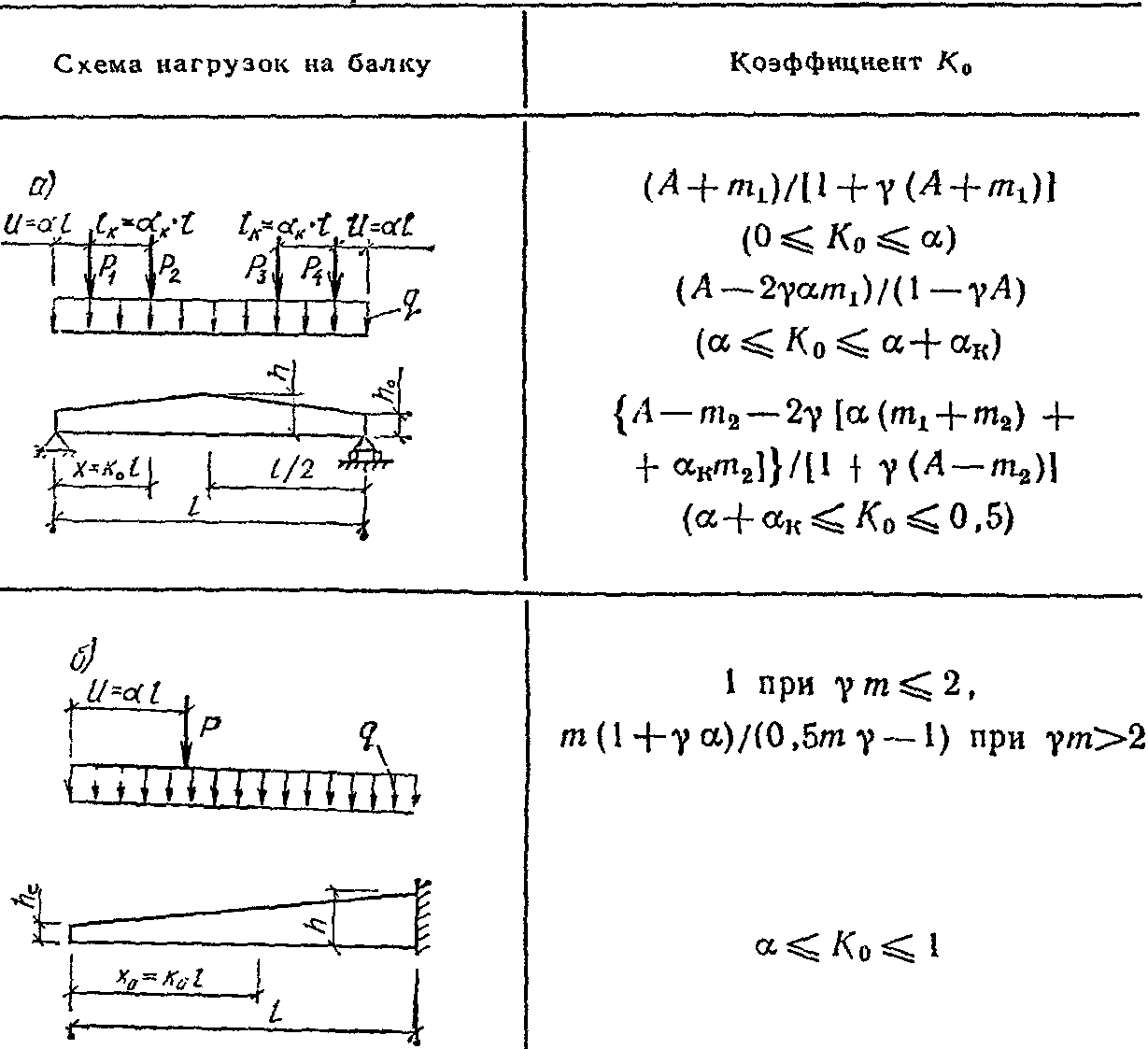 68
68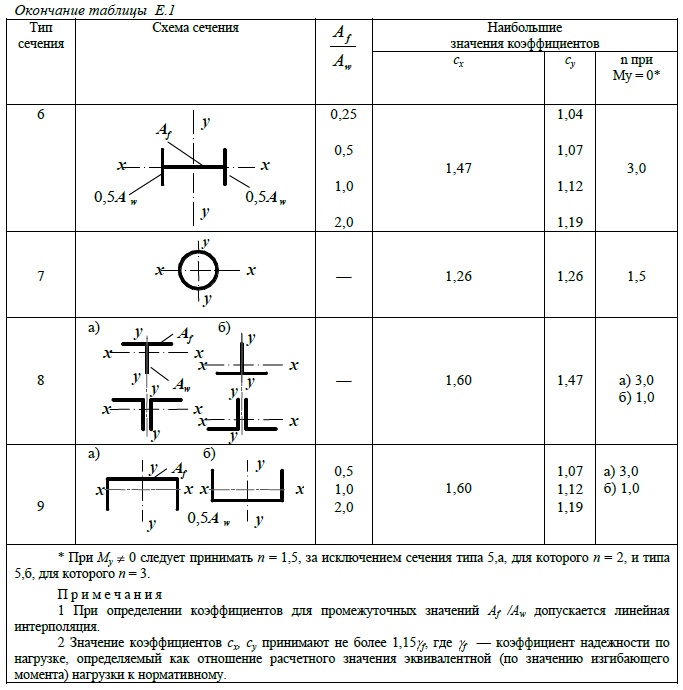 07
07